A geometry problem by Anthony Pham

Geometry Level 4

Observe net $ABCDEFGHIJ$ .

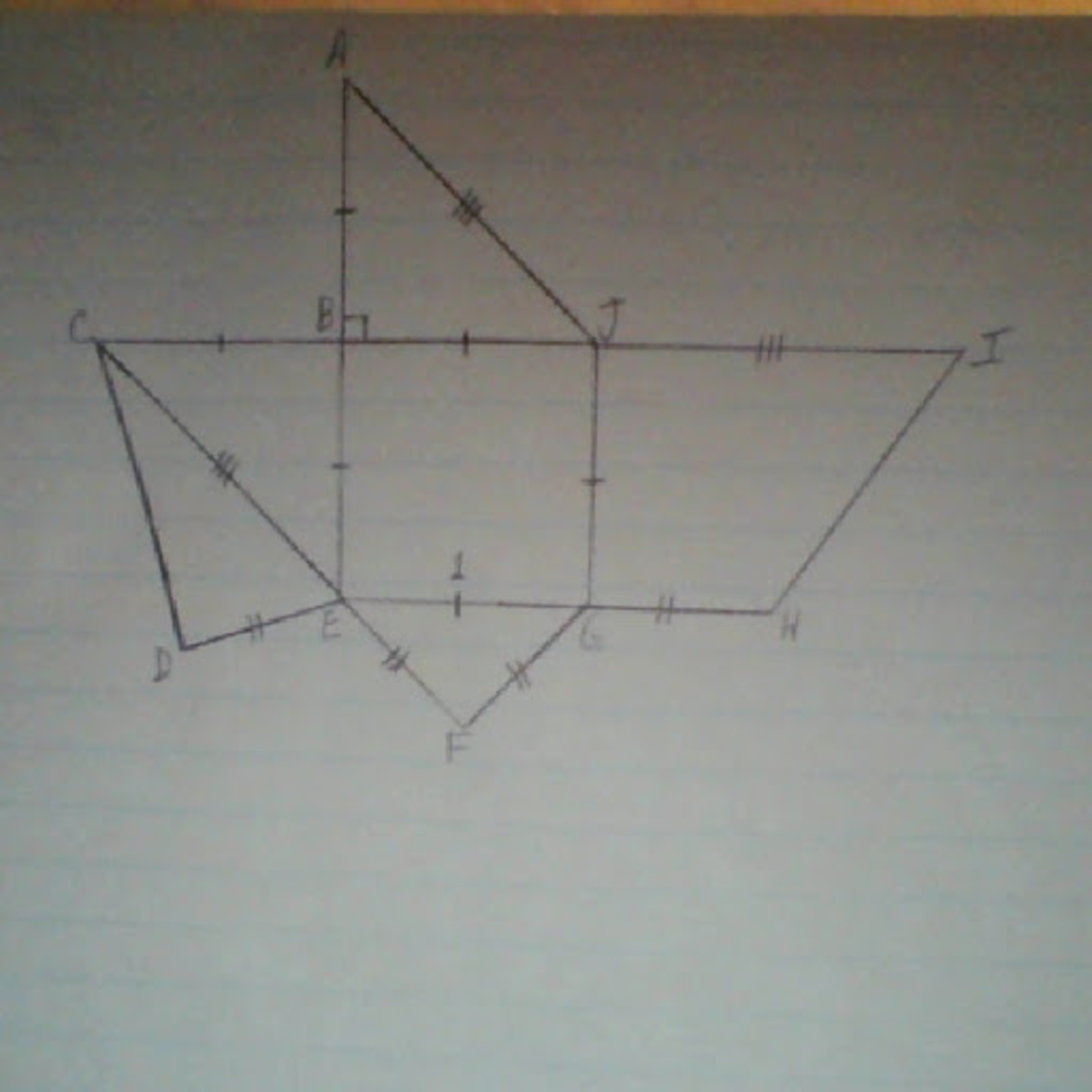
Figure $BEGJ$ is a unit square, with angle $ABJ=90^\circ$ and $BJ=AB=BC$ . Also, $DE=EF=FG=GH$ and $CE=AJ=JI$ , with the ratio of $GH$ to $IJ$ is $1:2$ . The net is to form a closed polyhedron no holes or overlaps. If the volume is written as a fraction in lowest terms, find the sum of the numerator and the denominator.

The answer is 17.

1 solution

Bob Kadylo
Sep 7, 2018

The closed polyhedron has 6 vertices in 3D space: A,C,I come together at (0,0,1), B is (0,0,0), E is (0,-1,0), G is (1,-1,0), J is (1,0,0) and D,F,H come together at (.5,-1,.5). I then sliced the solid with a plane through points A, E and G. The part with a square base had area 1 and volume $\frac{1}{3}$ .

The part with a triangle base AEG and apex F had a volume of $\frac{1}{12}$ . Total volume is $\frac{5}{12}$ . Answer is $\boxed{17}$

A geometry problem by Anthony Pham

The answer is 17.

1 solution

0 pending reports