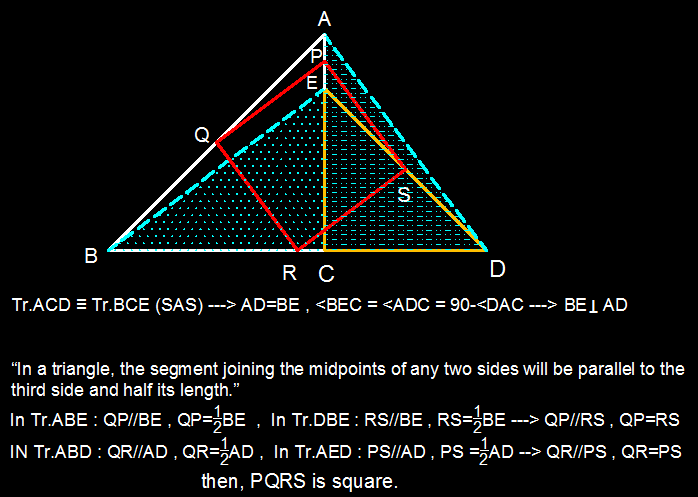
A geometry problem by Áron Bán-Szabó
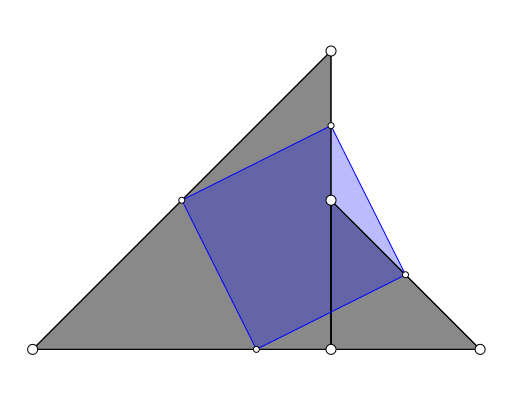
The two gray triangles are isosceles and right-angled. The midpoints of the quadrilateral defined by the triangles define the blue quadrilateral. Is the blue quadrilateral always a square?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
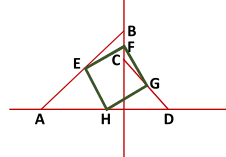
Equation of the line A B can be written as y = a + a x and that of the line C D as y = b − b x .
Coordinates of the midpoints then are
E = ( − 2 a , 2 a ) , F = ( 0 , 2 a + b ) , G = ( 2 b , 2 b ) , H = ( 2 b − a , 0 )
For simplicity of calculations it is possible to double all these coordinates. If the double sized object is a square, the original had to be a square as well.
E ′ = ( − a , a ) , F ′ = ( 0 , a + b ) , G ′ = ( b , b ) , H ′ = ( b − a , 0 )
The squares of pairwise distances are
E ′ F ′ 2 = a 2 + ( a + b − a ) 2 = a 2 + b 2
F ′ G ′ 2 = b 2 + ( b − a − b ) 2 = a 2 + b 2
G ′ H ′ 2 = ( b − a − b ) 2 + b 2 = a 2 + b 2
H ′ E ′ 2 = ( b − a + a ) 2 + a 2 = a 2 + b 2
So all the sides are the same length.
The pairwise slopes are
m E ′ F ′ = a b
m F ′ G ′ = b − a = − b a
m G ′ H ′ = − a − b = a b
m H ′ E ′ = b − a + a − a = − b a
So there are two pairs of parallel lines at right angles to each other.
The quadrilateral E F G H is therefore a square.