A geometry problem by Ashraful Mahin

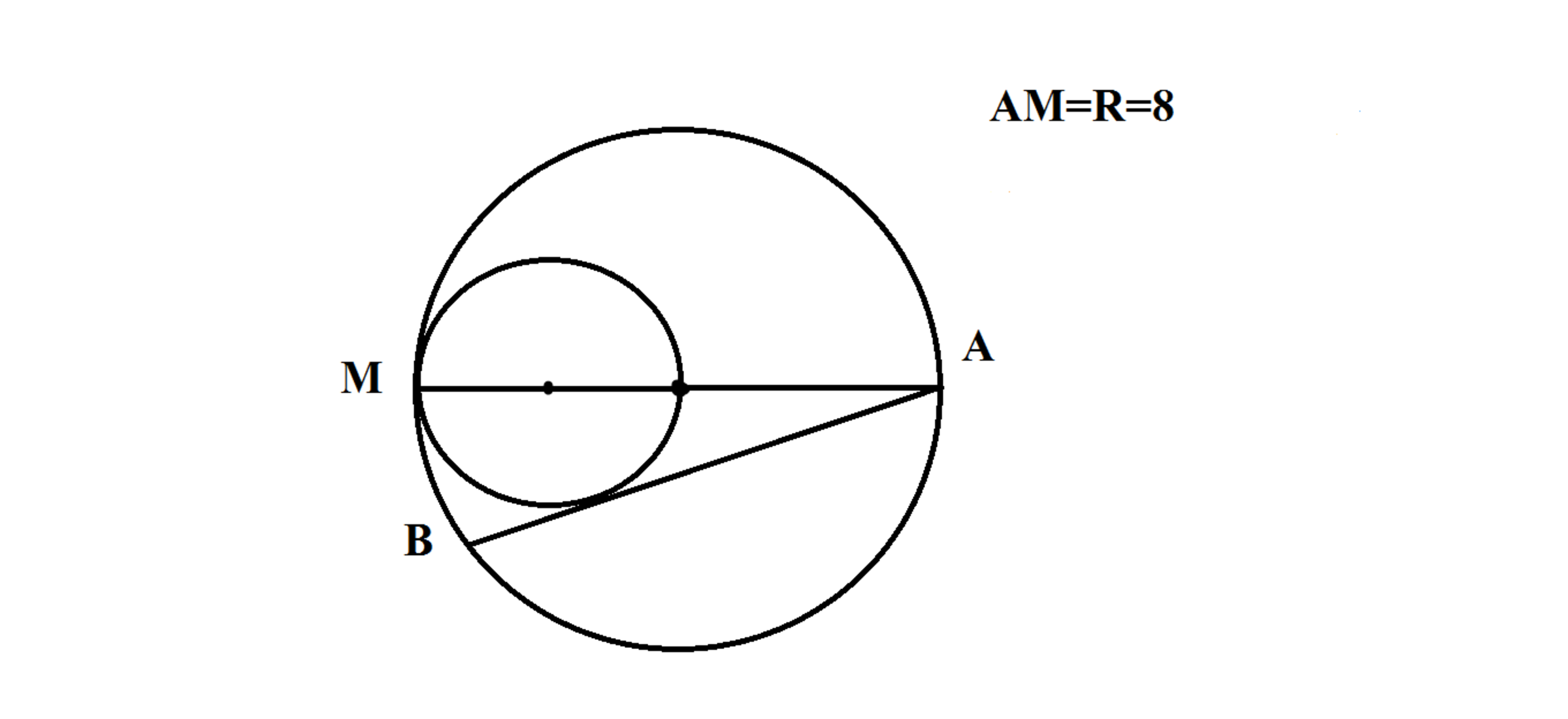
Two circles touch internally at point $M$ and the radius of the larger circle is 8 units. The centre of the larger circle lies on the perimeter of the smaller circle. The diameter of the larger circle that passes through the touching point M meets the larger circle at point $A$ . Tangent drawn from $A$ to the smaller circle touches that at $B$ . Length of $AB$ is of the form $\dfrac ab \sqrt2$ , where $a$ and $b$ are coprime positive integers, find $a-b$ .