A geometry problem by A Former Brilliant Member
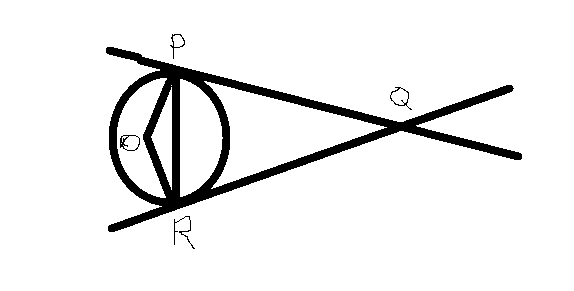 In the given figure, O is the center of the circle. Find the measure of angle PQR given angle POR=120.
In the given figure, O is the center of the circle. Find the measure of angle PQR given angle POR=120.
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
It should be mentioned that O is the center of circle or OP is the radius because the figure itself is vague.
 Consider the diagram. A tangent line to a circle makes a
9
0
∘
angle with the radius at the point of contact. The sum of the interior angles of a quadrilateral is
3
6
0
∘
. Thus,
Consider the diagram. A tangent line to a circle makes a
9
0
∘
angle with the radius at the point of contact. The sum of the interior angles of a quadrilateral is
3
6
0
∘
. Thus,
∠ P Q R = 3 6 0 − 9 0 − 9 0 − 1 2 0 = 6 0 ∘
Tangents make 90 degrees with circle and hence left out angle is 60 degrees
Angle POR = 120° ......(given) the tangent is always perpendicular to the radius, hence, Angle OPQ = 90°, Angle ORQ = 90°, so measure Angle PQR + OPQ + ORQ + PQR = 360...............(sum of measure of angles of a quadrilateral), hence, 120° + 90° + 90° + PQR = 360°, On solving this we get, measure angle PQR = 60°
PQ & RQ are tangents therefore OPQ= 90 & ORQ=90
there fore OPQR is a quadrilateral = 360
PQR= 360 - 120 - 90 - 90
PQR= 60
it should be mentioned that o is the centre of circle.
the touching PQ , QR makes 90 degrees with the radius PO,RO then 360 -(QPO + QRO+POR) = PQR THEN 360-(120+90+90) = 60