A geometry problem by aziz alasha

Geometry Level 4

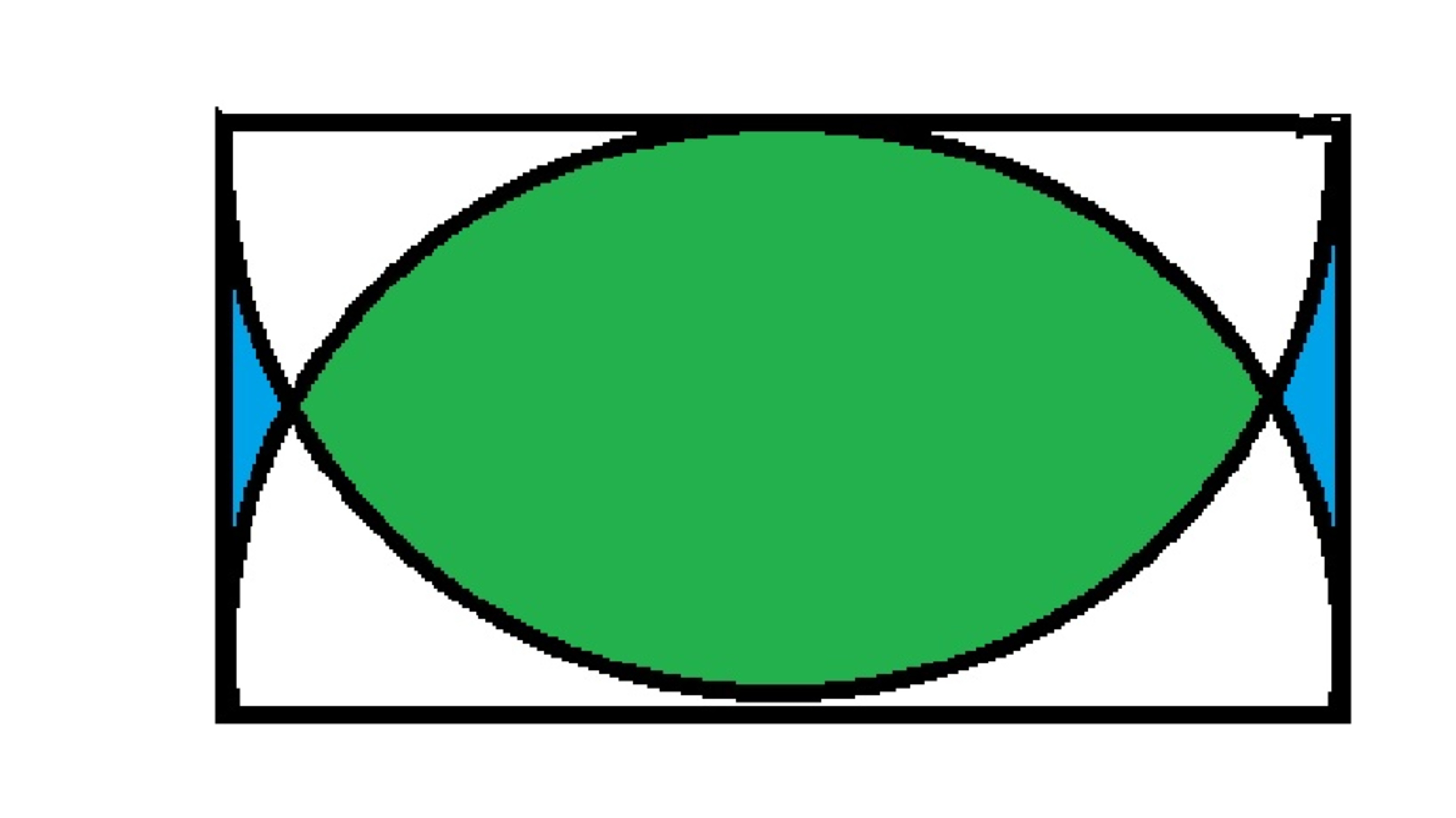
The figure above two similar semicircles of radius $R$ inscribed inside a rectangle.

Let the area of the green region and blue region be denoted by $A_1$ and $A_2$ , respectively.

If the vaue of (A1-A2)/A1 equals $\dfrac{a\pi -b}{c\pi -d \sqrt d}$ , where $a,b,c,d$ are all integers with $d$ square-free, find $a+b+c+d$ .

The answer is 25.

1 solution

Aziz Alasha
Jan 3, 2017

From the figure , by using some geometrical concepts we will get the length of the chord GH = √3.R Area of the circular Segment GHN = ( θ/360 × π − sin(θ)2)× R2 , so far , A1/2 = R²(π/3 - √3/4) , A1 = 2R²(π/3 - √3/4) then, Also the Area of the circular segment ABGH = πR²/2 – A1/2= R²(π/2 - π/3 + √3/4 ) . ABGH = R²(π/6 + √3/4 ) . Now , A2/2 = R² - R²(π/6+√3/4) = R²(-π/6-√3/4+1). then, 2R²(-π/6-√3/4+1) = A2 .
from previous results A1-A2 = 2R²(π/2-1) . A1 = 2R²(π/3-√3/4). Hence : (A1-A2)/A1 = (π/2-1)/ (π/3-√3/4) = (6π-12)/(4π-3√3) Therefore, a+b+c+d = 6+12+4+3= 25 .

the correct answer is 25 as shown , on the solution provided

Aziz Alasha - 4 years, 5 months ago

A geometry problem by aziz alasha

The answer is 25.

1 solution

0 pending reports