A geometry problem by Benjamin Jones
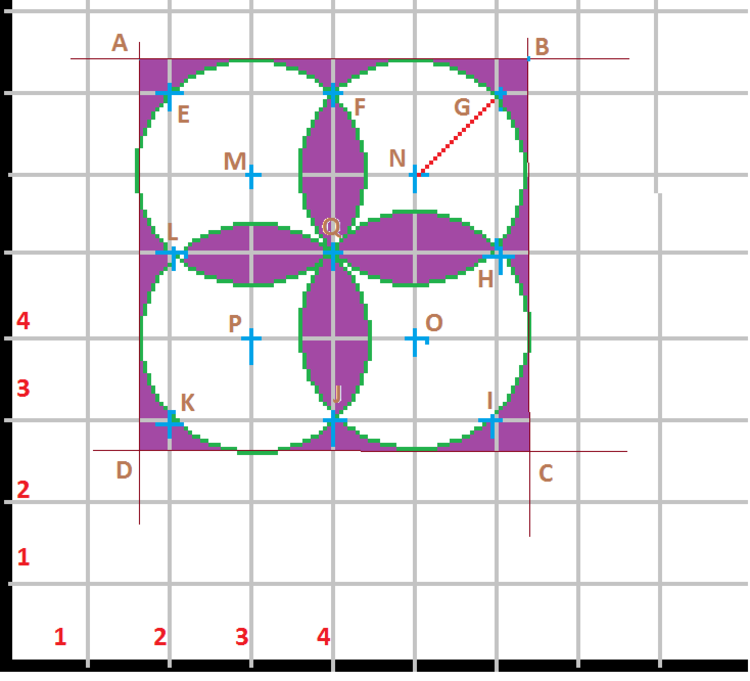 Find the area in purple given:
Find the area in purple given:
The distance between M and P is the same as the distance between P and O: 2 units.
Circles M,N,O, and P have equal radii and intersection Q.
Square ABCD is tangent to the circles.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The total purple area may be found as the "difference" between the areas of two squares of the radii 2+2sgrt2 and 4, because the inside purple area when equally decomposed fills eight white segments of the circles. You will then immediately get the correct answer.