I have no idea how I got this circle wedged in this parabola!
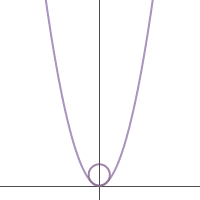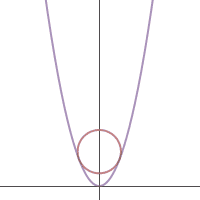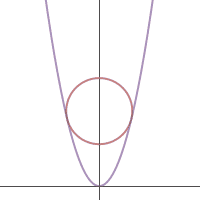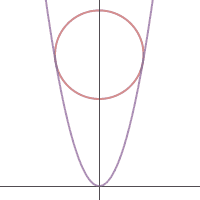 A parabola defined by the equation
y
=
x
2
is tangent to a circle at exactly two different points, and does not intersect the circle at any other points.
A parabola defined by the equation
y
=
x
2
is tangent to a circle at exactly two different points, and does not intersect the circle at any other points.
If the area of the circle is 9 π , what is the y-coordinate of the center of the circle?
The answer is 9.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Very nice. Related question: what is the largest circle that can be "dropped into" this parabola so that it falls to the bottom?
The radius and location of the circle are determined by the tangency with the parabola, so we should find the intersections of their graphs, y = x 2 and ( y − a ) 2 + x 2 = r 2 where a is the y-coordinate of the center of the circle, and r is the radius of the circle.
( x 2 − a ) 2 + x 2 = r 2 x 4 − 2 a x 2 + a 2 + x 2 = r 2 x 4 − ( 2 a − 1 ) x 2 + a 2 − r 2 = 0
Using the quadratic formula to find x 2 ,
x 2 = 2 1 ( ( 2 a − 1 ) ± ( 2 a − 1 ) 2 − 4 ( a 2 − r 2 ) )
x 2 = a − 2 1 ± r 2 − a + 4 1
x = ± a − 2 1 ± r 2 − a + 4 1
By inspection, the only way for there to be two and only two different roots is if the determinant of the original quadratic formula is zero.
r 2 − a + 4 1 = 0
a = r 2 + 4 1
It is simple to verify that these two intersections are indeed points of tangency. This last equation gives us the y-coordinate of the center of the circle as a function of radius. If the area of the circle is 9 π , then the radius must be 3 . This gives us a y-coordinate of
a = 9 . 2 5
At point ( x , y ) the slope of the parabola is 2 x (differentiate y = x 2 ).
The radius of the circle is perpendicular to the parabola at that point, so it has slope − 1 / 2 x .
The slope of the radius is − d / x so d = 1 / 2 .
Then x 2 + d 2 = R 2 , so y = x 2 implies y = R 2 − 0 . 2 5 and the y-coordinate of the center of the circle is R 2 + 0 . 2 5 .
Plugging in R = 3 gives the answer 9 . 2 5 .