Familiar Triangles
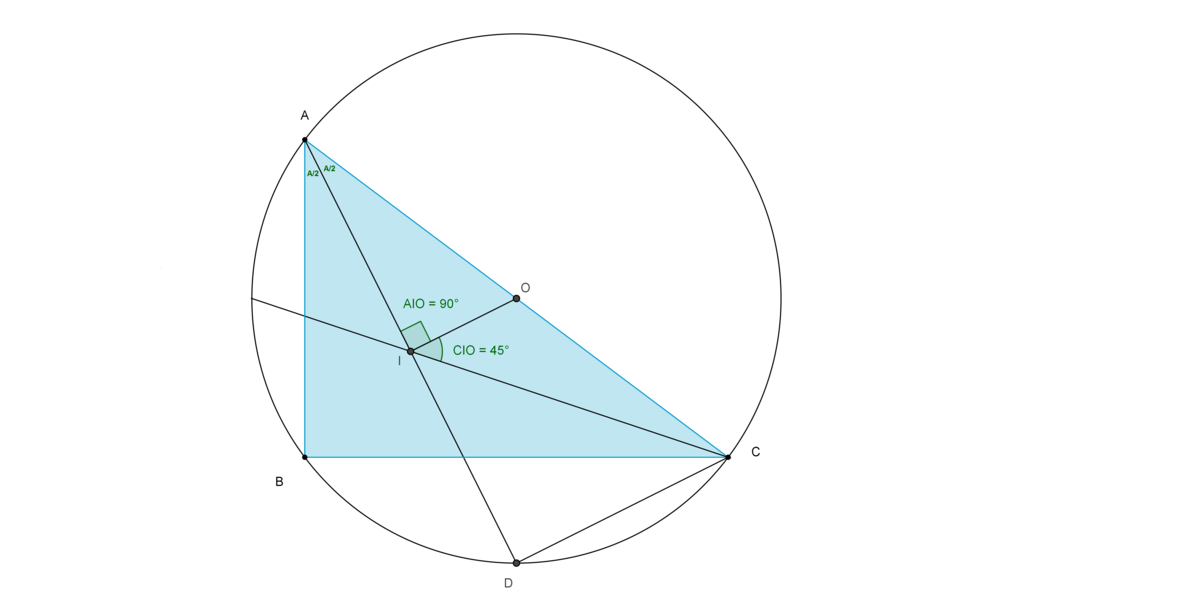
△ A B C with incentre I and circumcentre O is such that ∠ A I O = 9 0 ∘ and ∠ C I O = 4 5 ∘ . Find B C A B
The answer is 0.75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
S O L U T I O N :
Observe that ∠ A I C = 9 0 ∘ + 2 ∠ B ⇒ 1 3 5 = 9 0 + 2 ∠ B ⇒ ∠ B = 9 0 ∘ .
Then draw the circumcircle of △ A B C . Because ∠ B = 9 0 ∘ , AC will be the diameter.
And in a right angled triangle The circumcentre will be the midpoint of the hypotenuse.
Extend AI to meet the circumcircle at D. Then ID=DC. Moreover, △ A D C is similar to △ A I O (Common angle and 9 0 ∘ )
Thus by similarity we find that
D C = 2 I O and A D = 2 A I
A D = 2 A I ⇒ D I = A I .
D C = D I = A I
t a n 2 ∠ A = A D D C = 2 A I A I = 2 1
t a n ∠ A = 1 − t a n 2 ∠ A / 2 2 t a n ∠ A / 2 = 1 − 4 1 2 . 2 1 = 3 4
So, B C A B = t a n ∠ A 1 = 4 3 = 0 . 7 5
Nice Problem! I got another useful fact that the ratio r R = 2 5 .
Log in to reply
Yeah R=5x/2 and r=(3x+4x-5x)/2= x which implies R/r = 5/2.
First observe that ∠ B = 9 0 ∘ because ∠ C I A = 9 0 + 2 ∠ B ⇒ 1 3 5 = 9 0 + 2 ∠ B ⇒ ∠ B = 9 0 ∘ .
Let D be a point on A C such that I D is ⊥ to A C . Let R be the circum-radius and r be the in-radius.
A O = R , I O = R 2 − 2 R r (Well known fact), I D = r , A I = 2 R r .
Now △ A D I is similar △ A I O .
So, I O I D = A O A I ⇒ R 2 − 2 R r r = R 2 R r . After some algebraic manipulation, we get r = 5 2 R .
Now let E be a point on A B such that I E is ⊥ to A .
We get A I = 5 2 R , I E = r , so A E = 5 4 R by applying Pythagoras Theorem in △ A I E . Then B E = r = 5 2 R . So, A B = 5 6 R .
We also know that A C = 2 R . So we get B C = 5 8 R by again applying Pythagoras Theorem in △ A B C .
Therefore B C A B = 4 3 .