A geometry problem by Chung Kevin
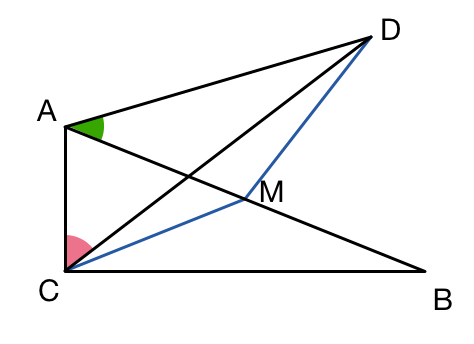
A B C is a right triangle with ∠ A C B = 9 0 ∘ . M is the midpoint of A B , and D is a point such that M C = M D with points C and D lying on opposite sides of A B , as shown in the diagram.
If ∠ D A B = 4 0 ∘ , what is ∠ D C A ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I tried to hide the fact that M is the circumcenter of the cyclic quad :)
Seems like most people missed it, because it wasn't clearly presented that way.
Log in to reply
Yes, that fact was well-disguised. This is the type of problem where the answer seems so obvious a f t e r you have solved it, but takes a while to get to that point. I noticed that A C B D was cyclic fairly quickly, but then for some reason it took me some time before I noticed that ∠ D A B = ∠ D C B . I think the blue lines were distracting my eyes from this fact. So I ended up chasing angles for a while before I first came up with the 5 0 ∘ answer in a roundabout way.
how is |AM|=|BM|=|MC|=|MD| , i could not this point ?
Log in to reply
Because ABC is a right triangle, we know that the circumcenter of ABC coincides with the midpoint of AB (which is M).
Then, we are given that M C = M D , so M is the circumcenter of these 4 points.
it was never mentioned why AM=CM ...
if you imagine that this shape is a shape with two headed arrows D and B. When it is folded the line AC is created. This means that angle DAB=Angle DCB= 40 so angle DCA= 90-40=50.
That is a good intuition, and it turns out to be true. However, you still have to explain why we get such a symmetric figure.
Put am=MB=L, CB=N and Cm=y. cos (b)=(N÷(2.L))={N^2+L^2-y^2}÷{2.N.L}. so L^2=y^2 so L=y ,,,,,,@∆ AMD , am=MD so. Angle (M D A) =40° and <AMD =100°. @∆ MCA cm=ma ,put Angle Mac=MCA=t and <CMA=u so U=180-2.t ,so Angle CMD=100+180-2.t=280-2.t ,,@∆ CMD Angle MCD= MDC =(180-(280-2.t))÷(2)=t-50°. so required Angle (ACD)=k=t-(t-50)=t-t+50 so k=50°########
As △ A B C is right triangle, we have M A ≅ M B ≅ M C ≅ M D , therefore quadrilateral A B D C is cyclic, hence ∠ A D B = 9 0 ∘ and ∠ D C A = ∠ A B D = 5 0 ∘
Know AM = MB = MC = MD. Triangles CDM, CMB, AMD, and CMA are all isosceles.
Angles ADC + ACD + CAD = 180.
Angle ADC = 40 - CDM. Angle ACD = ACM - DCM. Angle CAD = CAM + 40.
Substitute into second line.
(40 - CDM) + (ACM - DCM) + (CAM + 40) = 180.
80 - CDM - DCM + ACM + CAM = 180.
Since CDM = DCM and CAM = ACM,
2(ACM) - 2(DCM) = 100.
2(ACM - DCM) = 100.
ACM - DCM = 50.
As M is the midpoint of A B , we have that ∣ A M ∣ = ∣ B M ∣ = ∣ M C ∣ = ∣ M D ∣ . So M is the center of a circle on which A , B , C and D lie. Then as both ∠ D A B and ∠ D C B are subtended by the same chord D B , we have that ∠ D C B = ∠ D A B = 4 0 ∘ .
Finally, as Δ A B C is right-angled at C we see that ∠ D C A = 9 0 ∘ − ∠ D C B = 5 0 ∘ .