A geometry problem by Chung Kevin

$\large \tan~45=\dfrac{2}{x}$ $\color{#D61F06}\huge \implies$ $\large x=\dfrac{2}{\tan~45}=2$

$\large 2x=2(2)=4$

$\large A=\dfrac{1}{2}bh=\dfrac{1}{2}(4)(2)=$ $\color{plum}\boxed{\large 4}$

Since the triangle is isosceles and right, the base angles measure $45^\circ.$ The altitude is perpendicular to the base, so this means that the smaller triangles are also isosceles right.

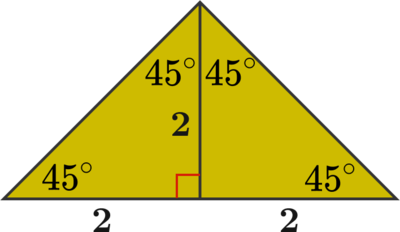
This means that the length of the base is 4, and so the area is

$\frac{1}{2}(4)(2)=\boxed{4}.$

The two triangles can be combined to form a square with sides of length 2.

as this is a isosceles right triangle,

so,the other angles will be 45.

now,if we think the whole triangle is divided into 2 by the height(line), then the 2 partitions are also isosceles right triang

so, the two triangle can make a squre of side 2.

Then the area is 2x2=4

Two triangle can make a squre of side 2 Then the area is 2x2-4

Can be transformed in a square with 2 units edge! 2*2 ...

Rotate the right hand half of the triangle through 270 degrees anticlockwise. The angle in the top right hand corner is still a right angle, so it becomes a square of side 2.

(1/4)th of a square of side 4.

Because if you cut the isosceles triangle in half, the halves would become a equaliteral triangle therefore, each side would be 2cm long so the area of the whole thing is $2*2$ which equals to four which is the answer.