A geometry problem by Chung Kevin
In a unit square, two quarter circles are drawn, centered at two opposite vertices.
What is the area of the oval-shaped region?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Most efficient way to do.
Yep, the trick here is to see that we just need to subtract the unshaded area which is simple to calculate using symmetry.
Ah, good use of the principle of inclusion and exclusion to find the area.
Yes Thanks,I learned a NEw principles.
Two quarter circles cover the whole area once and overlap in the blue area covering it twice.
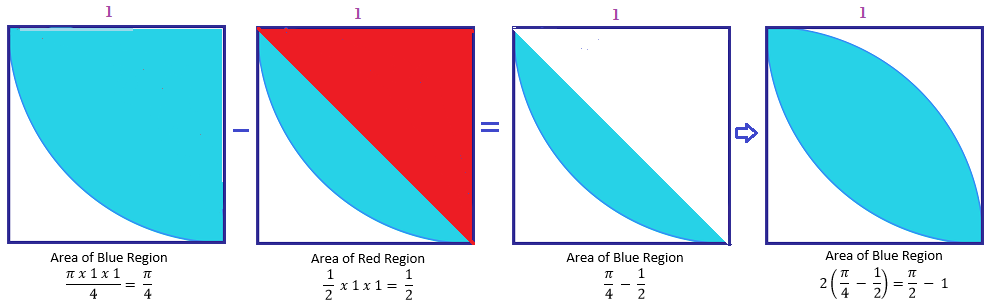
An area of two quarter circles minus an area of a square = area of half a circle minus a square = 2 π − 1 .
Elegant approach! It reminds me of the principle of inclusion and exclusion .
the area of the quarter circle is π/4 minus 1/2 the area of the square will give us half the blue area so π/4 - 1/2. the blue area is twice that or π/2 - 1
I was not as elegant in finding the solution, but I found it anyway. If you draw the a 1" radius circle inside a 2" square box, it's easy to find "0.570" as the solution.
Clearly the most elegant of the solutions.
You could just eyeball it. Option 1 is 2 - 1.57, so .43, Option 2 is .14. Option 3 is 1.57-1, or .57, and Option 4 is a number larger than 1. Since the area is 1 and the blue area is clearly about half, you can eliminate options 2 and 4. Then the question is is it closer to 60% blue or 40% blue. It is closer to 60%, so option 3.
I do not have such accurate eyeball skills. Moreover, most of the geometry problems don't have a properly scaled diagram, so eyeballing is not applicable in those cases.
This may not apply to most geometry problems, but it works in this case. When I zoomed out from the diagram it was clear that the larger part was blue. Precise calculations are often not required when you are given a multiple choice question.
By sight, the shaded oval is a bit more than half the area of the square which is 1. So the only answer that is a bit more than 0.5 is (pi/2)-1.
Imagine if you are solving this problem without given options, how would you solve this problem?
The blue area is equal to 2× [Area of the quarter circle - (1/2) area of the square] =
= The area of a semi-circle - The area of the square
= [(1/2)π(1)^(2)]-(1*1)
= (π/2)-1
Therefore the answer is (π/2) - 1
To clarify, "(1/2) area of the square" comes from the right triangle with the diagonal of the square as its hypotenuse.
The area of the quarter circle is 4 π .
Thus the area of the part of the square - quarter of circle is = 1 − 4 π , since there are two of these areas,
then the unwanted area is 2 − 2 π ⟹ the area of the oval part is 1 − ( 2 − 2 π ) = 2 π − 1
Firstly divide the oval region shaped into two halves then calculate the area of the triangle = 1/2(1)(1)=1/2
Then calculate the area of quadrant = (πr*2)/4 which is equal to = π/4 then
Subtract the both area =(π/4 - 1/2 )
This is the area of 1/2 Oval shaped and multiplied by 2 == (π/2-1)
This is a nice way to look at the blue area, like a triangle removed from a quadrant.
Technically, that shape is called a vesica piscis - or you could just say the football-shaped region if you want to use a more familiar term. Oval is not a well-defined term, so fine, call I guess you can call it an oval. But I don't think this shape matches the common usage of the term.
I didn't know that name. I learn something new!
It's too pointed at the end to truly be an oval.
Your solution is hard to understand. What is α in this context? What has been substituted?
Method 1: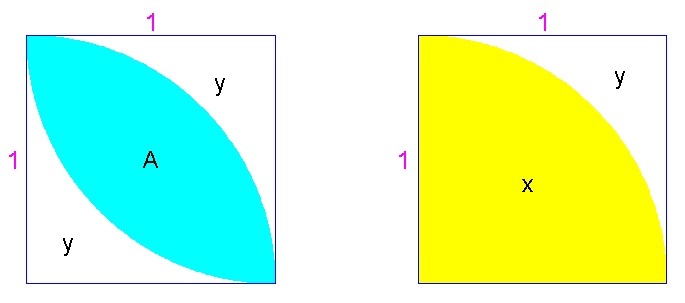
let A be the area of the oval-shaped region, x be the area of the quarter circle (yellow region) and y be the area of the white region
then,
x = 4 1 ( π ) ( 1 2 ) = 4 π
it follows that,
y = 1 2 − 4 π = 4 4 − π
Finally,
A = 1 2 − 2 ( y ) = 1 − 2 ( 4 4 − π ) = 1 − ( 2 4 − π ) = 1 − 2 + 2 π = − 1 + 2 π = 2 π − 1 answer
Method 2: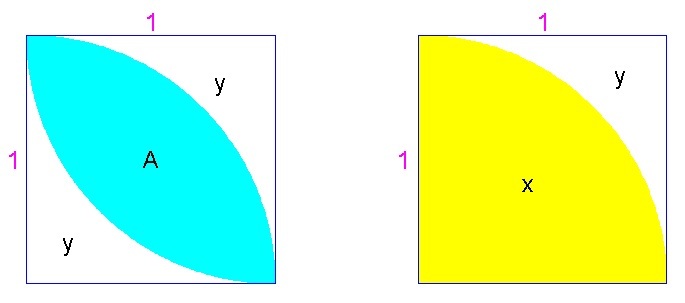
let A be the area of the oval-shaped region, x be the area of the quarter circle (yellow region) and y be the area of the white region
then,
x = 4 1 ( π ) ( 1 2 ) = 4 π
it follows that,
y = 1 2 − 4 π = 4 4 − π
Finally,
A = x − y
A = 4 π − 4 4 − π
A = 4 π − ( 4 − π )
A = 4 π − 4 + π
A = 4 2 π − 4
A = 4 2 π − 4 4
A = 2 π − 1 answer
Method 3: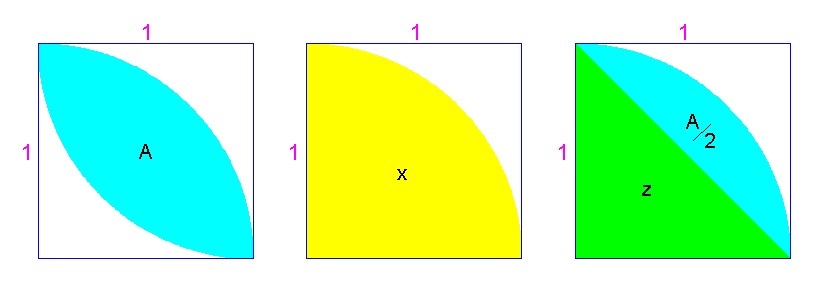
let A be the area of the oval-shaped region, x be the area of the quarter circle (yellow region) and z be the area of the triangle (green region)
then,
x = 4 1 ( π ) ( 1 2 ) = 4 π
it follows that,
z = 2 1 ( 1 ) ( 1 ) = 2 1
then,
2 A = x − z
2 A = 4 π − 2 1
Finally,
A = 2 ( 2 A ) = 2 ( 4 π − 2 1 ) = 2 π − 1 answer