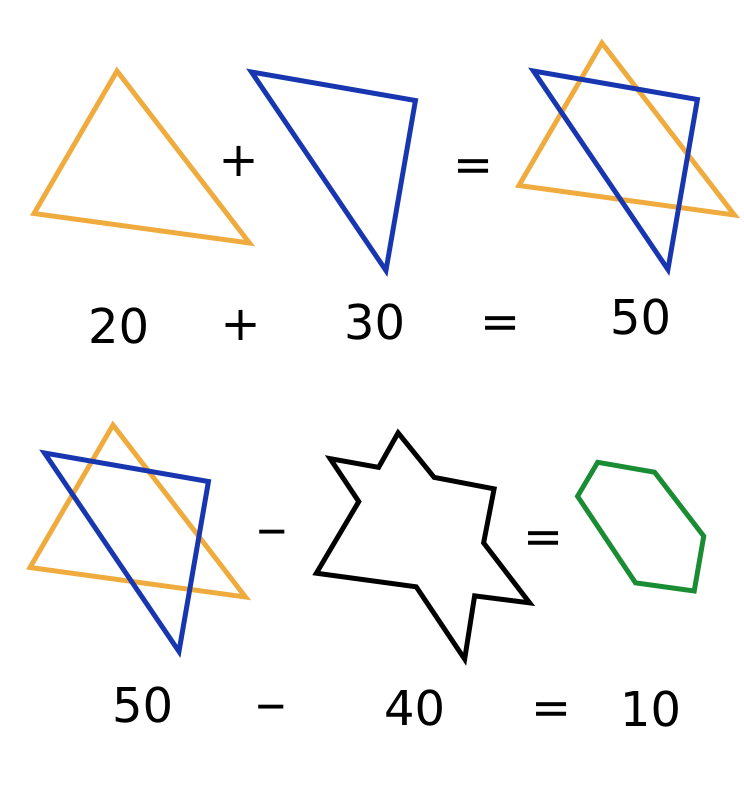
A geometry problem by Chung Kevin

$20 + 30 = 50$

$50 - 40 = 10$

Need pictures to explain I guess.

Edit:

You can use set theory for this.

Perimeter of the green hexagon is A (intersection) B

A U B is the star of David.

A U B = A + B - A (intersection) B

A (intersection) B = A + B - (A U B) = 20 + 30 - 40.

In the hexagon three sides are shared by the yellow triangle and other three are forming triangle with the yellow one , so according to triangle rule sum of two sides should be greater than third one , therefore Hexagon's perimeter should be less than yellow triangle perimeter, and in our options 10<20 is the only wise one

The picture shows that the green perimeter is part of the yellow perimeter, and therefrore has to be les than 20. Ed Gray

Though it's an older problem, I wanted to add a solution myself since the figure might throw off a couple of people. The math is of course quite simple: The perimeter of the two triangles together is 50 (30+20) and the perimeter of the star is 40. If you trace the star with a pen, you will notice that exactly the hexagon in the middle is left over, therefore its perimeter is 10 (50 - 40).

What is rather obvious from the figure, is that this figure definetly does not show a situation like that. It is far too close to a regular 6 spiked star. In a regular 6 spiked star formed of two equlateral triangles, the perimeter of the star is equal to 2/3 times the perimeter of the two triangles which is given by 6 times the sides or mathematically:

p(star) = 2/3x2x3xs = 4s

For the hexagon in the middle the perimeter is then obviously 1/3 times the perimeter of the two triangles:

p(hexagon) = 1/3x2x3xs = 2s

The perimeter of the hexagon is half of the stars perimeter. For any figure that is too close to the regular six spoked star this will roughly be true. Hence many people would intuitively guess that the hexagon might have half the perimeter of the star, which in my opinion reflects an interesting basic understanding of math that is more helpfull in everyday life than calculating something exactly. But yes, calculating something exactly is also helpfull.

If we add the perimeters of the blue polygon and the yellow polygon, that is equal to the perimeter of the hexagon plus the outside perimeter of the figure.

20 + 30 = perimeter of hexagon + 40

50 = perimeter of hexagon + 40

50 - 40 = perimeter of hexagon

10 = perimeter of hexagon

The Star perimeter (S) = Yellow perimeter (Y) + Blue perimeter (B) - Green perimeter (G) because G does not form part of S. Thus, 40 = 20 + 30 - G and G = 50 - 40 = 10

A. Ferguson, UK.

do you mean the perimeter of blue triangle is 30? 40=(20-x)+(30-y), x+y=20+30-40, x+y=10