Walk From My House
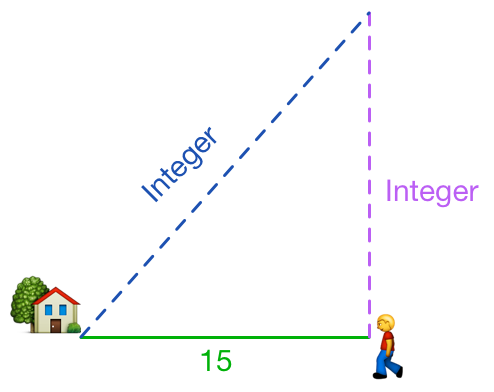
From my house, I walked 15 miles East and then turned North. What is the minimum integer distance (in miles) that I have to walk further, such that my distance (in miles) from the house is also an integer?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Using the Pythagorean Theorem, if we denote the vertical distance in miles as a and the hypotenuse in miles as b , then 1 5 2 + a 2 = b 2 .
Rearranging yields a 2 − b 2 = − 2 2 5 ⇒ ( a + b ) ( a − b ) = − 2 2 5
Now we can factorise − 2 2 5 as − ( 5 2 × 3 2 ) , and a + b and a − b will have to use all these factors between them. Since a and b are both positive, the second bracket ( a − b ) in our equation must be negative. Also, ∣ a + b ∣ > ∣ a − b ∣ , so now there are just two cases to try:
- a + b = 2 5 , a − b = − 9
- a + b = 7 5 , a − b = − 3
The first case gives the desired answer a = 8 . The second gives another solution of a = 3 6 , but this is not the minimum distance so is not what we need.
Method 01 : Apply Pythagorean theorem :
Let the vertical distance be denoted as x and the hypotheniuse be denoted as y , then by Pythagorean theorem , we have 1 5 2 + x 2 = y 2 , where x and y are positive integers.
So we want to minimize the value of x such that y is still an integer.
We can apply trial and error for x = 1 , 2 , 3 , … to get the smallest solution of x = 8 and that will be the answer.
Method 02 : Apply the parametric equations for Pythagorean theorem :
If all the sides of a right triangle are integers, they will satisfy the parametric triplets: ( m 2 − n 2 , 2 m n , m 2 + n 2 ) .
and if one of the sides (that is not a hypothenuse) is an odd number, in this case, it's 15, then m 2 − n 2 = 1 5 = 1 6 − 1 = 4 2 − 1 2 ⇒ m = 4 , n = 1 , thus the other (non-hypothenuse) side is equal to 2 m n = 2 × 4 × 1 = 8 .