A geometry problem by Chung Kevin

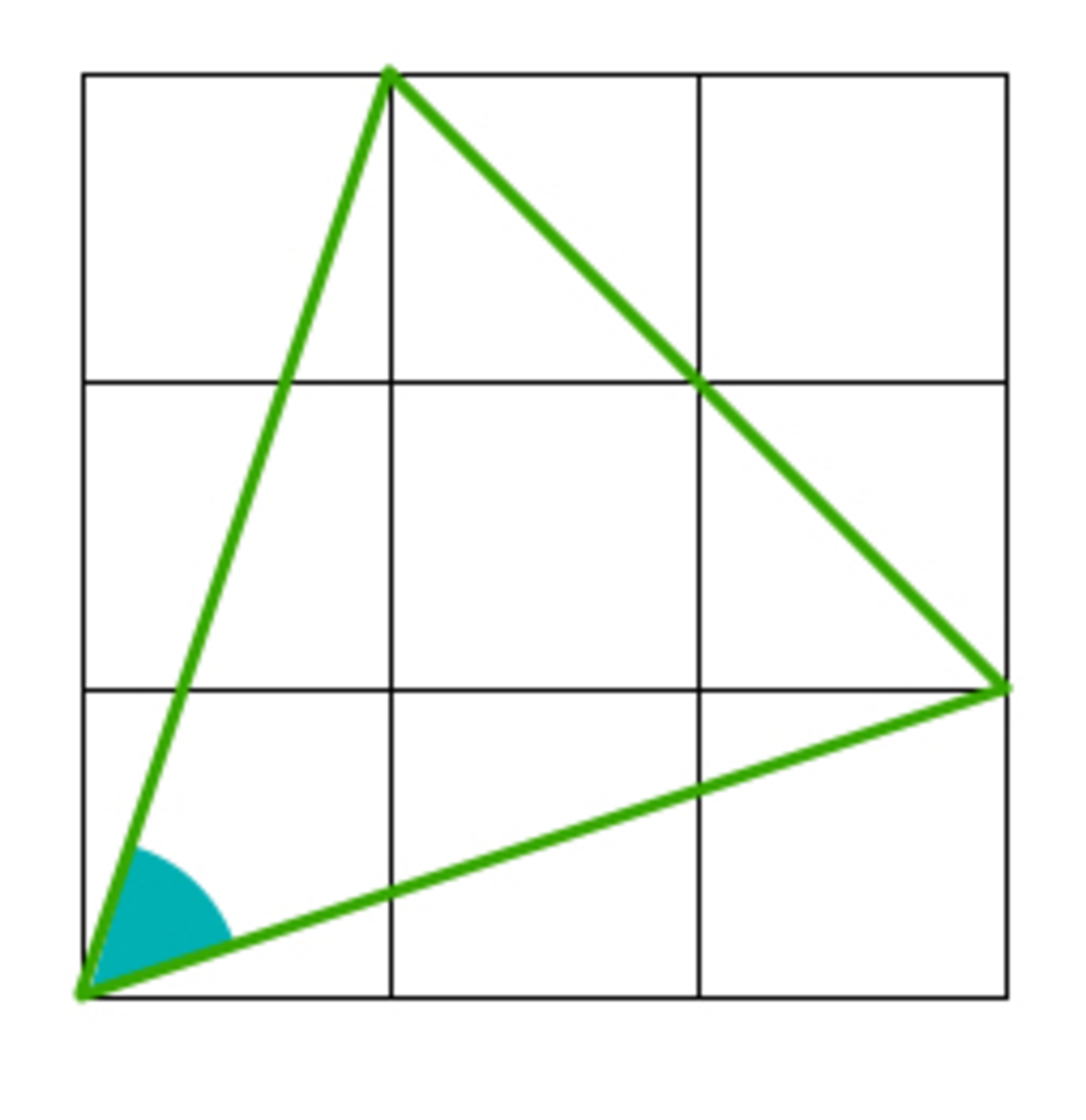
Let the measure of the blue angle be $\theta$ . Then we note that $\tan \dfrac \theta 2 = \dfrac 12$ . Therefore, $\tan \theta = \dfrac {2\times \frac 12}{1- \left(\frac 12 \right)^2} = \dfrac 43$ and $\theta = \boxed{\tan^{-1} \dfrac 43}$ .

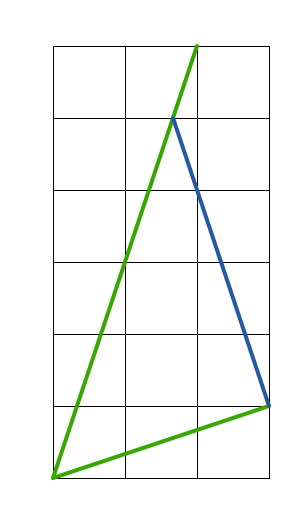
The special property of the green lines is that they are slanted "1 square for every 3 squares". This suggests that we could use a different coordinate axis system to try and get a better sense of the angle.

From the lower green line, we create the coordinate axis by drawing the blue line at a slope of "1 square for every 3 squares". This will intersect the upper green line again. By doing a bit of algebra, we can see that they intersect at $(\frac{5}{3}, 5 )$ in the old coordinate axis.

From here, by counting the number of squares, we can see that we get a $3 - 4 -5$ triangle, and hence the angle is $\tan^{-1} \frac{4}{3}$ .