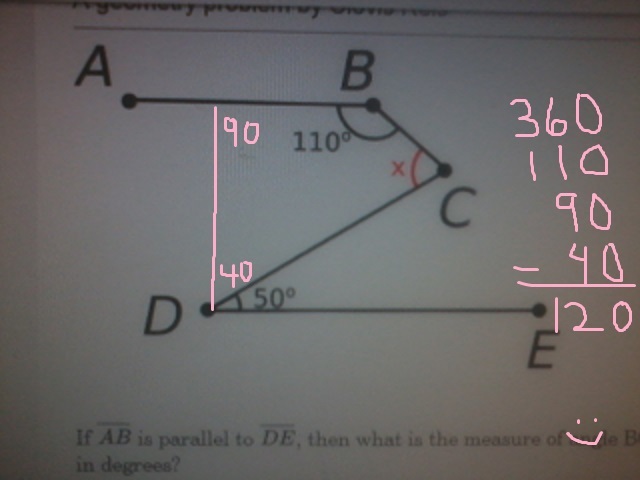
Angles in a Snakey Segment
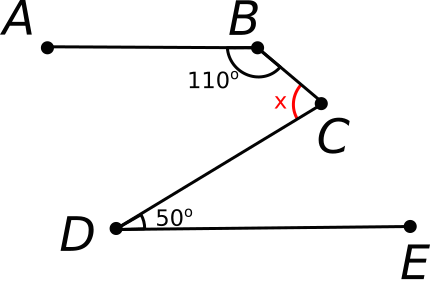
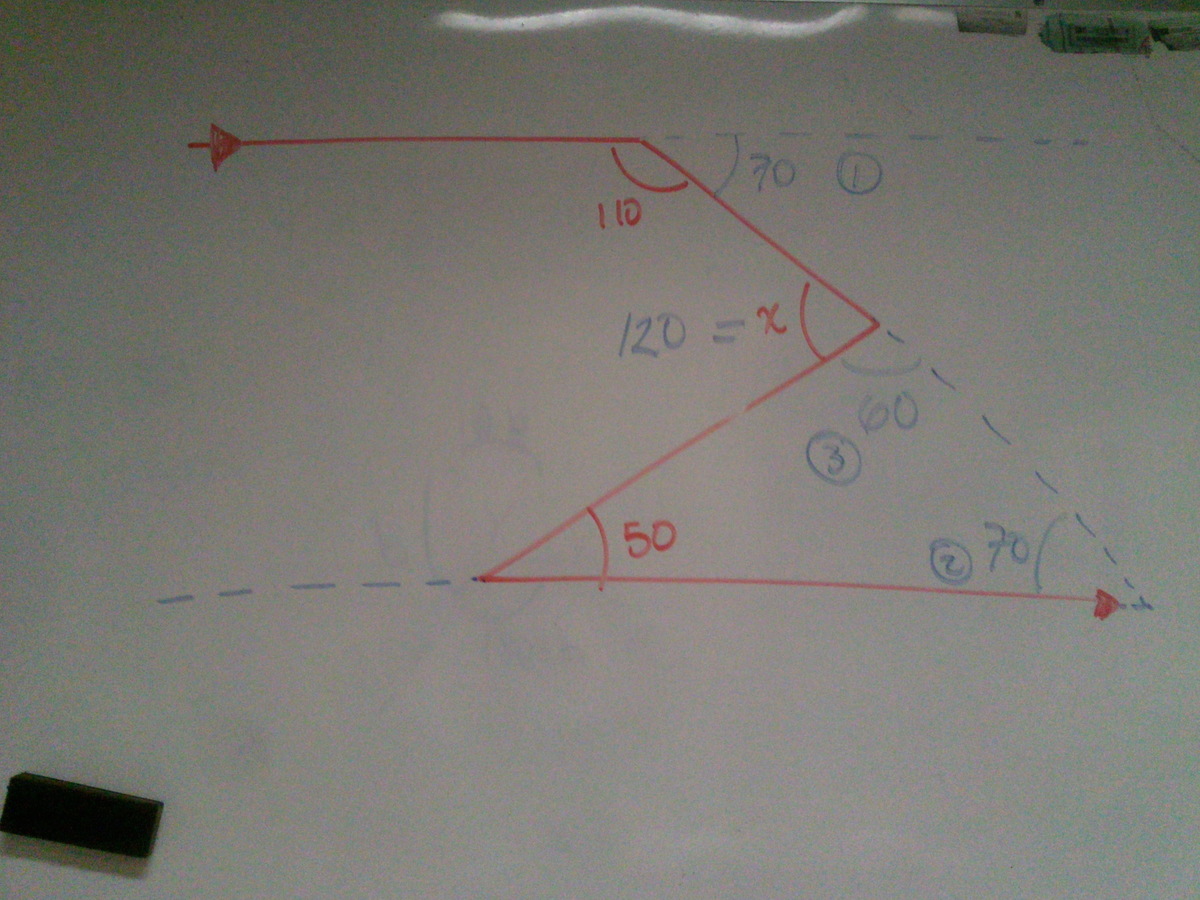
If A B is parallel to D E , then what is the measure of angle B C D in degrees?
The answer is 120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
Nice solution!
I also used a perpendicular line to solve this problem, only this looks much simpler than what I did as I drew my perpendicular line from point B creating two triangles that one could easily determine each of the angles created with a few minor calculations. However, I do like this answer as it is simple and very straight forward with little explanation needed
Log in to reply
Sometimes math is easier to understand that way :) Thanks!
it is the best &easiest solution.thanks a lot.
I used a perpendicular through C, but your solution is much more elegant.
I will add a line segment parallel with the line A B , D E called X C )
Then, ∠ X C D = 5 0 ° because ∠ X C D and ∠ C D E are alternate interior angles
Then ∠ B C X = 7 0 ° because ∠ X C B + ∠ A B C = 1 8 0 ° ( Consecutive interior angles )
Lastly, take 5 0 ° + 7 0 ° = 1 2 0 °
This is how I solved it.
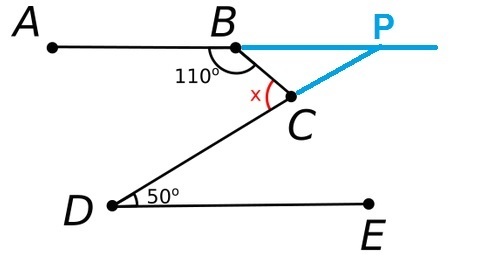
∠ C D E a n d ∠ B P C are alternate interior angles, so ∠ B P C = 50
Then ∠ P B C = 180 - 110 = 70
Then
∠
B
C
P
= 180 - 70 - 50 = 60
Finally x = 180 - 60 =
1
2
0
I take issue with this because visually, it's an acute angle.
Did the same thing
Angle APD is also 50 degrees. Angle PBC is 180 - 110 = 70. Therefore angle BCP is 180 - 120 = 60. Therefore BCD is 180 - 60 = Are you kidding me? 120!! Something's fishy because I agree it should be less than a right angle.
Did in the same way!
I also did it the same way. However, in the diagram, it appears to be an acute angle, not an obtuse angle👍
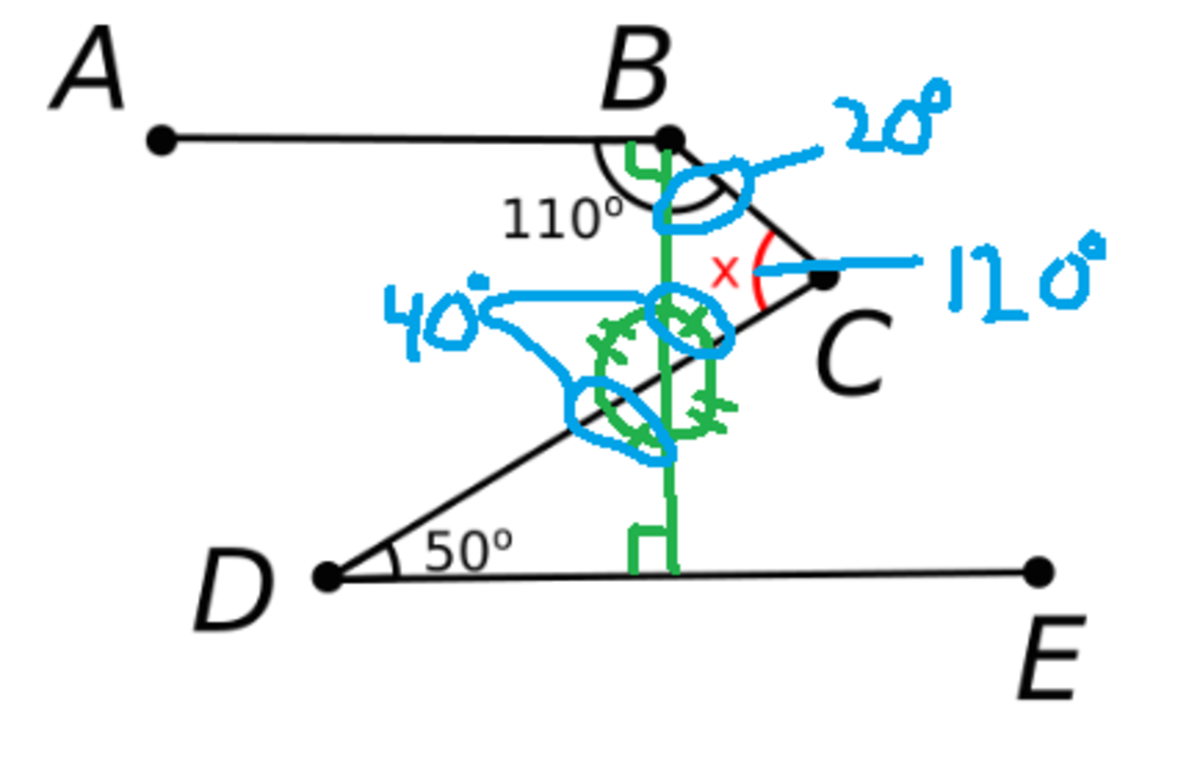
The is why I love math so much there are many different ways to solve problems like this. I personally drew a line perpendicular to line segment AB to create two triangles. The bottom triangle containing angle CDE and the newly created 90 degree angle allowed me to find the third angle of that triangle by subtracting those two angles from 180, since the sum of all interior angles of a triangle is 180 degrees. So 180-90-50=40, with this information I also know that the opposite angle from where this perpendicular line crosses line segment CD is also 40 degrees giving us one of the angle of the top triangle created. Now let's look at the other angle at point B, since I drew a perpendicular line from point B we can subtract 90 from 110 to discover the top angle of the top triangle, giving us 110-90=20. With this information we can now subtract the measurement of both of the new angles of the top triangle from 180 to give us the solution for what angle x is. This would be 180-40-20=120, so x=120.
The ans is 120, how ever the picture is a bit misleading. The angle does not look like 120, it looks like even less than 90 !
Problems are better if they have parallel solutions, :]
Am I the only one who did it this way? Draw a segment from A to D. This makes ABCD into a quadrilateral, therefore the total angles of ABCD = 360 degrees. We know <ADE+<BAD=180-50=130, while <ABC=110. Therefore, <BCD=360-130-110=120
I guess you are the only one who did it this way
Trace a line parallel to AB that cross the point C. Let’s call it XC where X is the leftmost point.
∠XCB + ∠ABC = 180° or 180° - ∠ABC =∠XCB
∠XCB = 180° - 110° = 70°
∠XCD = ∠CDE = 50°
∠BCD = ∠XCD + ∠XCB = 50° + 70° = 120°
Be F the point that DC intercepts AB, Angle BFC is 50º. Angle CBF is 180º - 110º = 70º. So angle BCF is 180º - 50º - 70º = 60º. Thus x = 180º - BCF = 180º - 60} = 120º
draw a st. line passing through c parallel to eother ab or de then get the sum of 50 and 70 to get your ans..simple
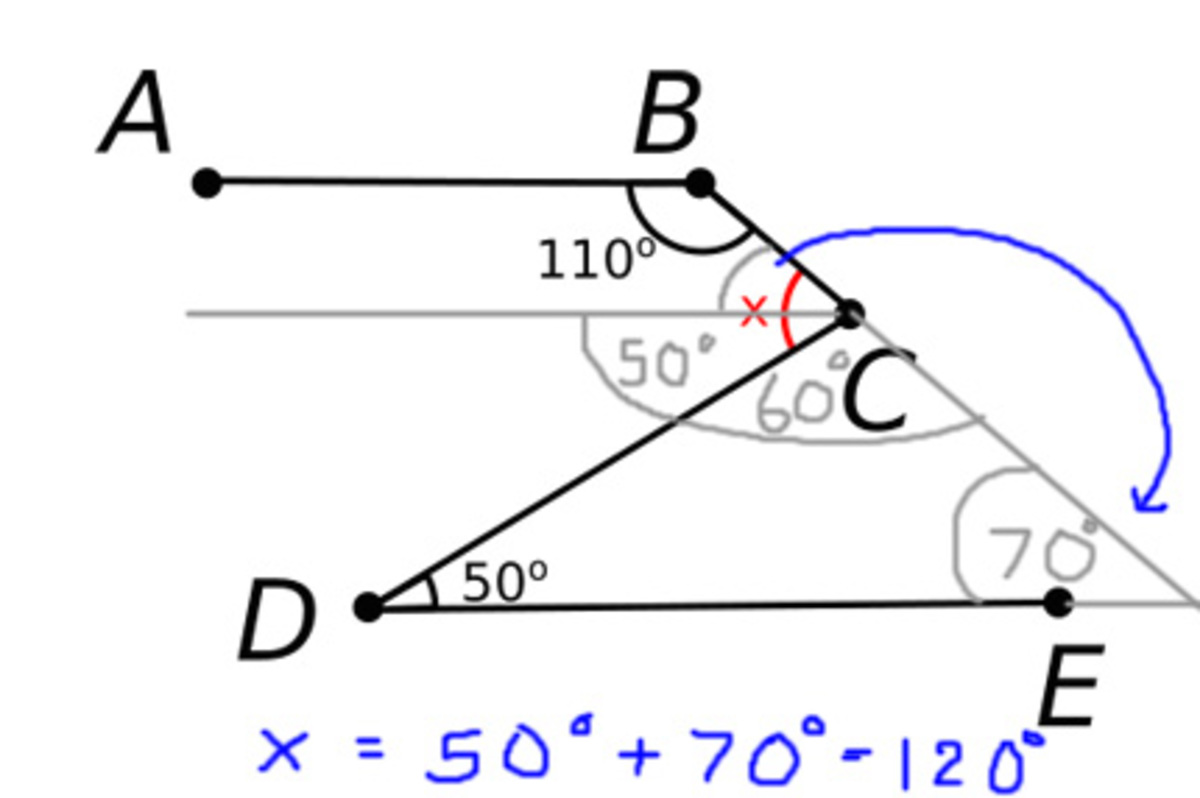

This is the easiest way: