Spiraling Triangles
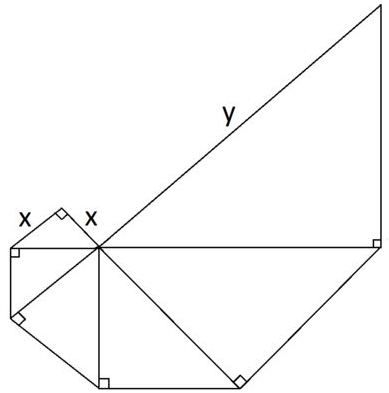
In the diagram above, each triangle is a right isosceles triangle. What is the value of y (in terms of x )?
Note: An isosceles triangle is a triangle in which two of the sides have the same length.
Bonus : What would the value of the largest side be if the spiraling pattern of right isosceles triangles established in the diagram was continued to include 14 triangles?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Your solution is beautiful and elegant but Can't we solve first few cases an make genral case using GP?
Log in to reply
Thank you. Yes - I think your idea of solving the general case using the geometric progression would lead to a more elegant solution- the bonus question would be a bit tedious otherwise. A formula for h n in terms of x would give a more general solution.
First, lets take notice that in an isosceles triangle the hypotenuse will always equal 2 × ( h y p o t e n u s e ) 2 .
Now, bearing that in mind, we can glide through that problem with that simple knowledge.
Let's calculate the first hypotenuse:
2 x 2 = x 2 .
Now, this being the leg of our next triangle, we'd use it to calculate the next hypotenuse. Then the next, and so on.
Hypotenuse of second triangle: 2 ( x 2 ) 2 = ( x 2 ) 2 .
Hypotenuse of third triangle: 2 ( ( x 2 ) 2 ) 2 = ( ( x 2 ) 2 ) 2 .
Have you noticed the pattern yet? We're just multiplying by 2 every time. In fact, we can even write up an equation to the find the hypotenuse of the nth triangle: h n = x 2 n .
So, for the problem above, we would just evalute h 6 .
h 6 = x 2 6 = x 2 6 = x ∗ 2 3 = 8 x .
As for the bonus:
h 1 4 = x 2 1 4 = x 2 1 4 = x ∗ 2 7 = 1 2 8 x .
Moderator note:
Great detailed solution.
I believe the answer to the bonus question can be expressed as 128x
Each inner edge has a ratio of 2 to the two shorter edges. There are 3 inner edges, so the answer is 2 6 = 8 .
First, we find the hypotenuse of the smallest triangle.
Let h 1 represent the length of the hypotenuse. Applying the Pythagorean theorem ,
x 2 + x 2 = h 1 2 , so h 1 = ( 2 ) x .
(We chose the positive solution since h 1 represents a length.) Next, let h 2 represent the hypotenuse of the next triangle (the triangles whose legs have length h 1 ). The Pythagorean Theorem gives ( 2 x ) 2 + ( 2 x ) 2 = ( h 2 ) 2 ,
which simplifies to 2 x 2 + 2 x 2 = ( h 2 ) 2 . Solving for the positive value of h 2 , we get h 2 = 2 x .
Next, let h 3 represent the hypotenuse of the triangle whose legs have length h 2 and apply the Pythagorean Theorem to this triangle to get ( ( 2 x ) ) 2 + ( ( 2 x ) ) 2 = ( h 3 ) 2 , or h 3 = 2 2 x . Continuing in this manner, a pattern emerges – each hypotenuse is 2 times the previous hypotenuse. In general, the hypotenuse of a right isosceles triangle is 2 times the length of one of its legs – our work finding h 1 demonstrates this. Thus, since the hypotenuse of a smaller triangle in the diagram is also a leg of the next larger triangle, the entries in the table can be found by multiplying the preceding entry by 2 .
Since y in the diagram represents the hypotenuse of the 6 th smallest triangle, we have y = 8 x .