A geometry problem by Deepansh Jindal

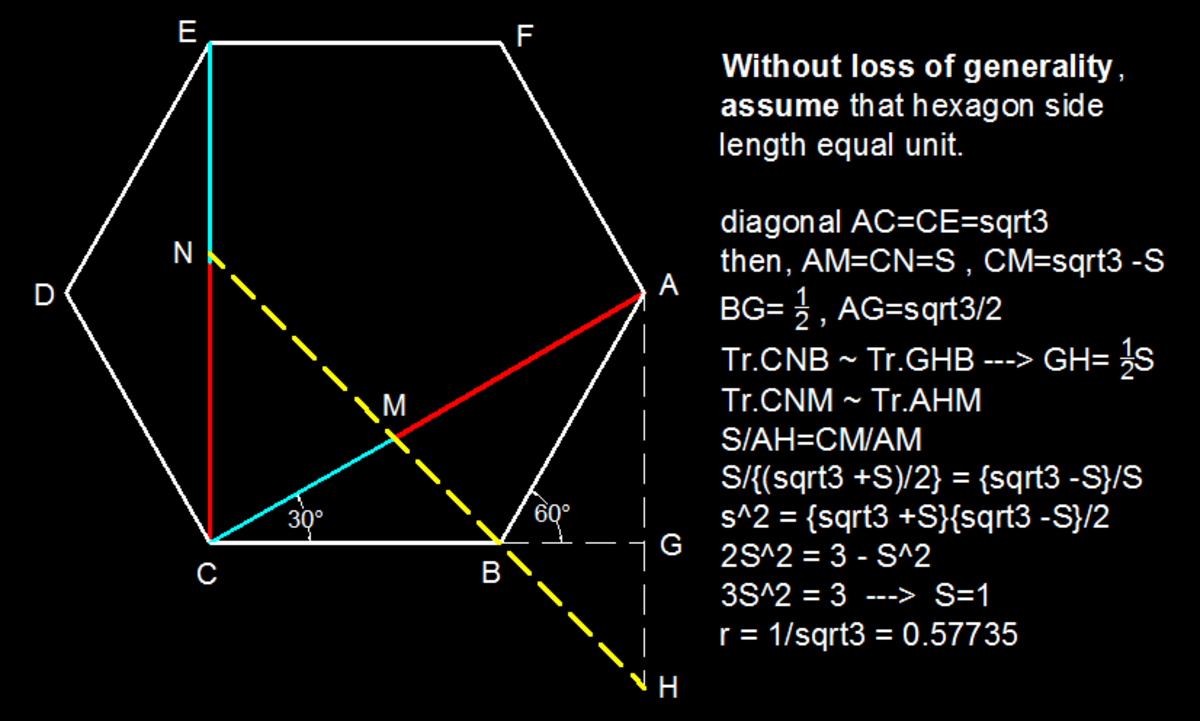
Suppose $X$ is the intersection of $AC$ and $BE$ . $X$ is the mid-point of $AC$ .

Since $B, M,$ and $N$ are collinear, then by Menelaus Theorem ,

$\dfrac{CN}{NE}\cdot\dfrac{EB}{BX}\cdot\dfrac{XM}{MC}=1.$

Suppose the side length of the hexagon is $1.$ Then $AC=CE=\sqrt{3}$ .

$\dfrac{CN}{NE}=\dfrac{CN}{CE-CN}=\dfrac{\frac{CN}{CE}}{1-\frac{CN}{CE}}=\dfrac{r}{1-r}$

$\dfrac{EB}{BX}=\dfrac{2}{\dfrac{1}{2}}=4$

$\dfrac{XM}{MC}=\dfrac{AM-AX}{AC-AM}=\dfrac{\frac{AM}{AC}-\frac{AX}{AC}}{1-\frac{AM}{AC}}=\dfrac{r-\frac{1}{2}}{1-r}$

Substituting them into the first equation yields

$\dfrac{r}{1-r}\cdot\dfrac{4}{1}\cdot\dfrac{r-\frac{1}{2}}{1-r}=1$

$3r^2=1$

Hence $r=\dfrac{\sqrt{3}}{3} \approx \boxed{0.57}$