Inspired by Keen Mun
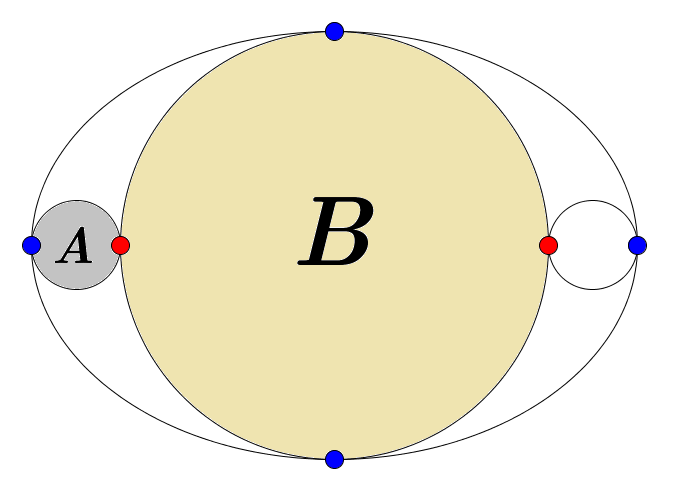 There are 1 bigger circle and 2 same size circles inscribed in an ellipse. The two red points are the foci of the ellipse. Find the ratio of areas
.
There are 1 bigger circle and 2 same size circles inscribed in an ellipse. The two red points are the foci of the ellipse. Find the ratio of areas
.
Give your answer to 3 significant figures.
The answer is 0.04289.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
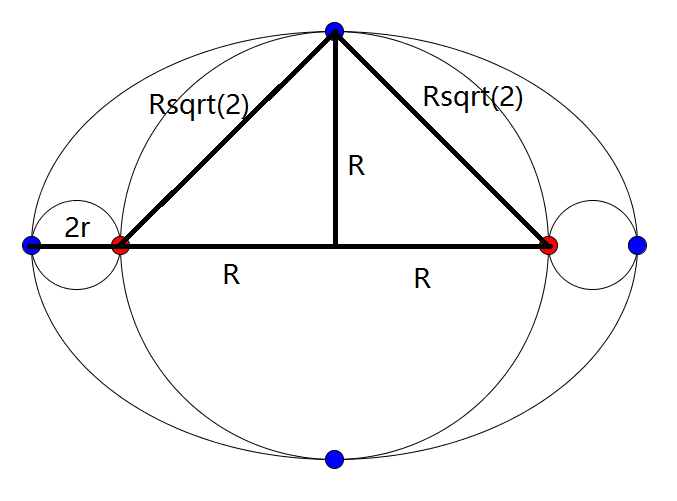
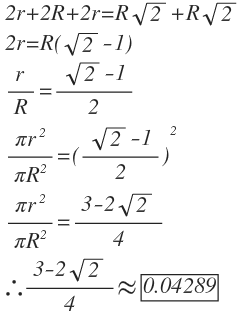
In normal notation, let a be semimajor axis, b semiminor axis and distance between focii as 2c. R A a n d R B t h e r a d i i . W e k n o w t h a t a 2 = b 2 + c 2 . B u t i n t h i s p r o b l e m R A = b = c , ⟹ a 2 = 2 R A 2 = 2 c 2 . ⟹ a = 2 ∗ R A . W e a l s o s a w c = R A . . . . . . ∗ . N o w h e r e w e h a v e 2 R B = a − c , ⟹ R B = 2 1 ∗ ( a − c ) = . . . . . ∗ 2 1 ∗ ( 2 R A − R A ) = 2 1 ( 2 − 1 ) R A . S o t h e r a t i o s o f a r e a s = π ∗ R A 2 π ∗ R B 2 = R A 2 { 2 1 ( 2 − 1 ) R A ) } 2 = 4 1 ∗ ( 3 − 2 2 ) . T h e r a t i o s o f a r e a s = 0 . 0 4 2 8 9 3 2