A geometry problem by Dexter Woo Teng Koon
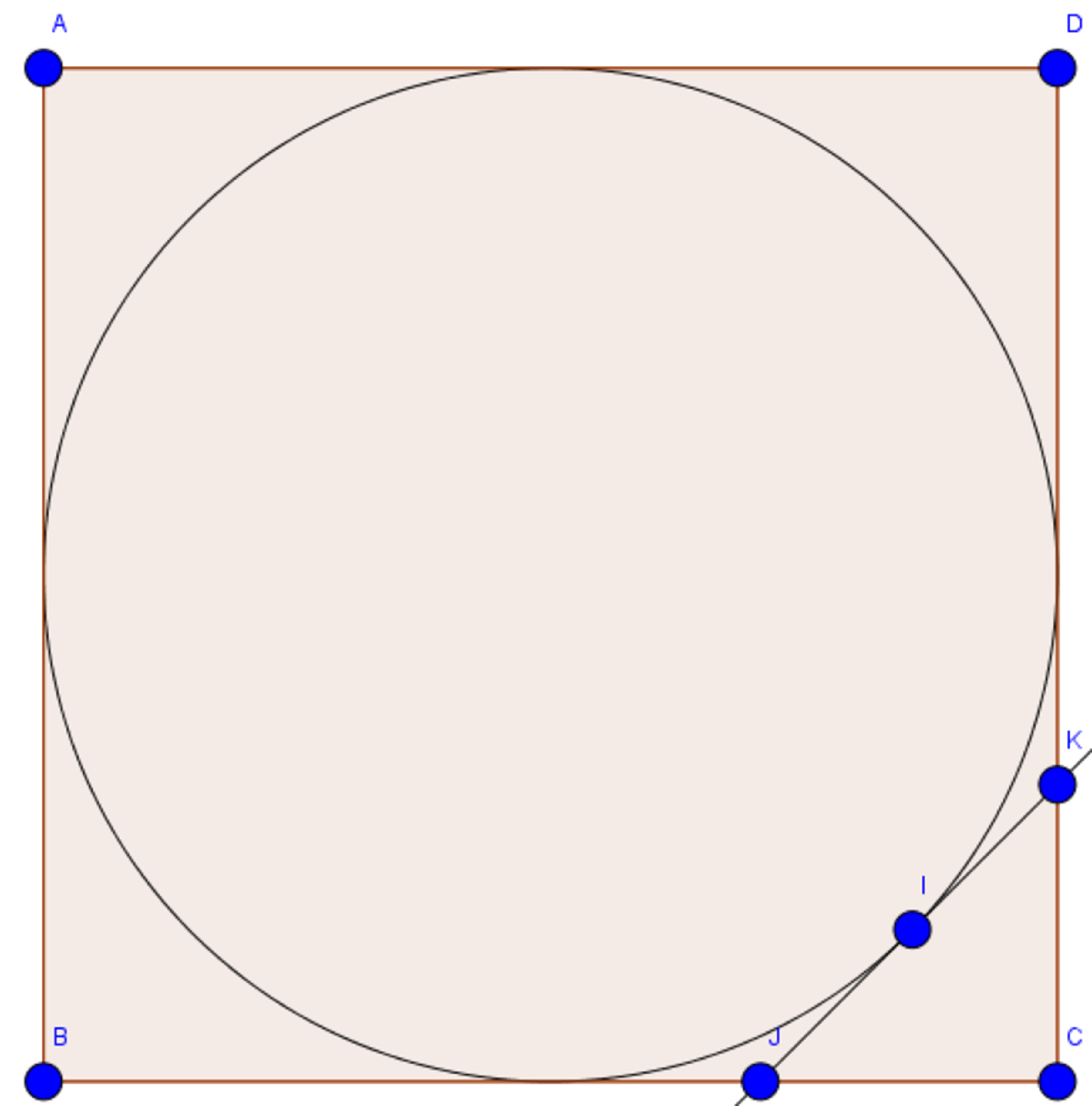
A circle is inscribed in a square A B C D , line J K is tangent to the circle at point I .
If 4 × J C = B C , then k × C K = C D .
Find k .
The answer is 3.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
 }
}
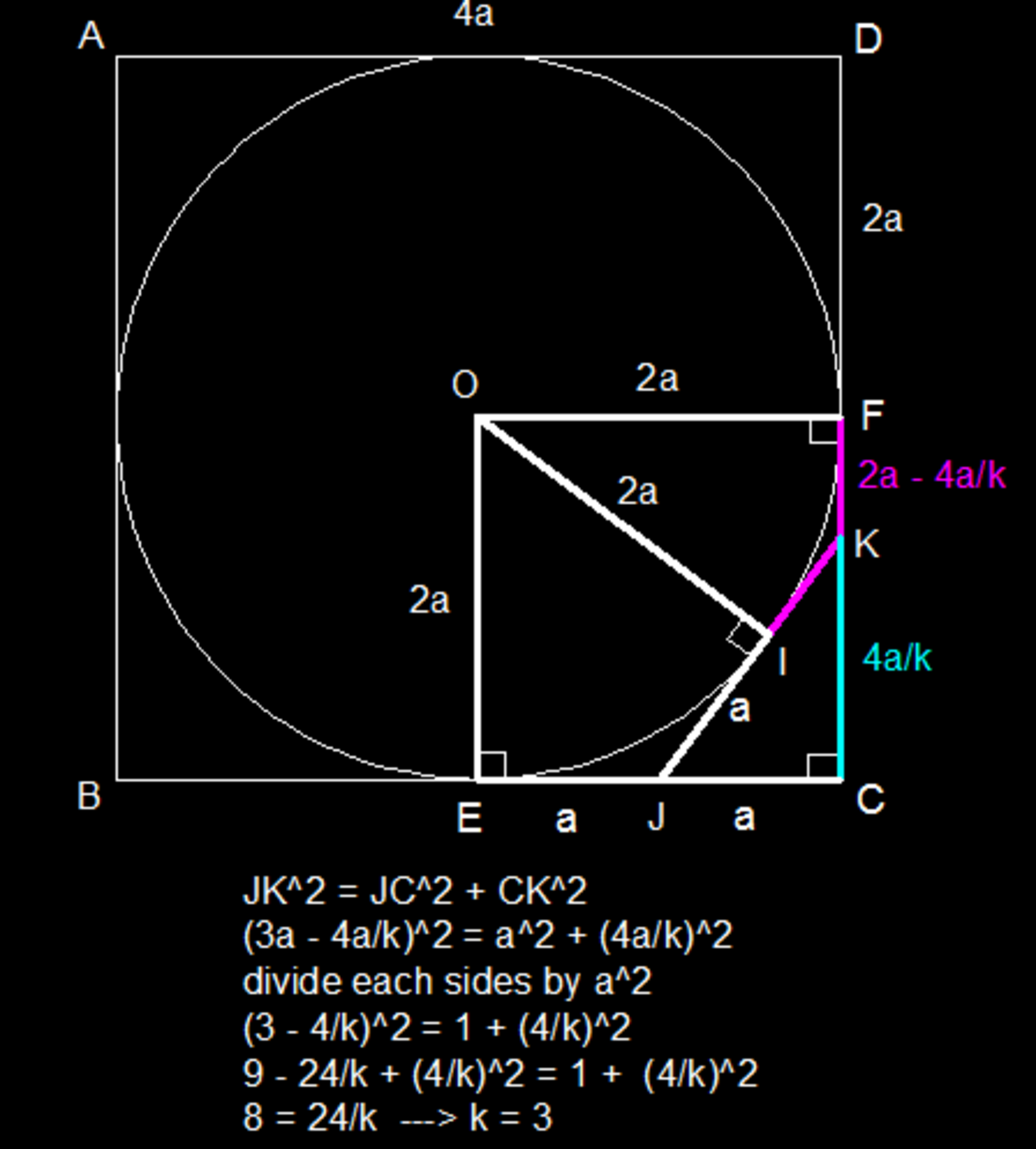
 Let
J
C
=
1
.
Let
J
C
=
1
.
∠ O J P = arctan 2 = 6 3 . 4 3 5 ∘
∠ K J C = 1 8 0 ∘ − 2 × 6 3 . 4 3 5 ∘ = 5 3 . 1 3 ∘
C K = tan 5 3 . 1 3 ∘ = 3 4
k = C K C D = 3 4 4 = 3
Here is why it comes out exact:
C K = tan ( 1 8 0 ∘ − 2 arctan 2 ) = − 1 − tan 2 ( arctan 2 ) 2 tan ( arctan 2 ) = − 1 − 4 2 × 2 = 3 4
Beatifull solution. +1).
Imagine a coordinate system with it's origin at the center of the circle. Then if
r
is the radius of the circle, the equation that describes the circle is:
x
2
+
y
2
=
r
2
Let
I
(
x
0
,
y
0
)
I
is a point of the circle. Therefore:
x
0
2
+
y
0
2
=
r
2
.....
(
1
)
The equation of the tangent line of the circle at point
I
is:
x
0
x
+
y
0
y
=
r
2
Let
J
(
x
1
,
y
1
)
It is obvious that
y
1
=
−
r
Also:
4
×
J
C
=
B
C
⇒
4
×
(
r
−
x
1
)
=
2
r
⇒
4
r
−
4
x
1
=
2
r
⇒
x
1
=
2
r
J
is a point of the tangent line. Therefore:
x
0
2
r
+
y
0
(
−
r
)
=
r
2
⇒
x
0
=
2
y
0
+
2
( 1 ) ⇒ ( 2 y 0 + 2 ) 2 + y 0 2 = r 2 ⇒ 5 y 0 2 + 8 r y 0 + 3 r 2 = 0 ⇒ y 0 = − a ( d e c l i n e d ) or y 0 = 5 − 3 r
x 0 = 2 y 0 + 2 ⇒ x 0 = 5 4 r
Thus, the equation of the tangent line is:
5
4
r
x
−
5
3
r
y
=
r
2
⇒
4
x
−
3
y
=
5
r
For
x
=
r
we have:
4
r
−
3
y
=
5
r
⇒
y
=
−
3
r
K C = r − ∣ y ∣ ⇒ K C = 3 2 r
k × K C = C D ⇒ k 3 2 r = 2 r ⇒ k = 3
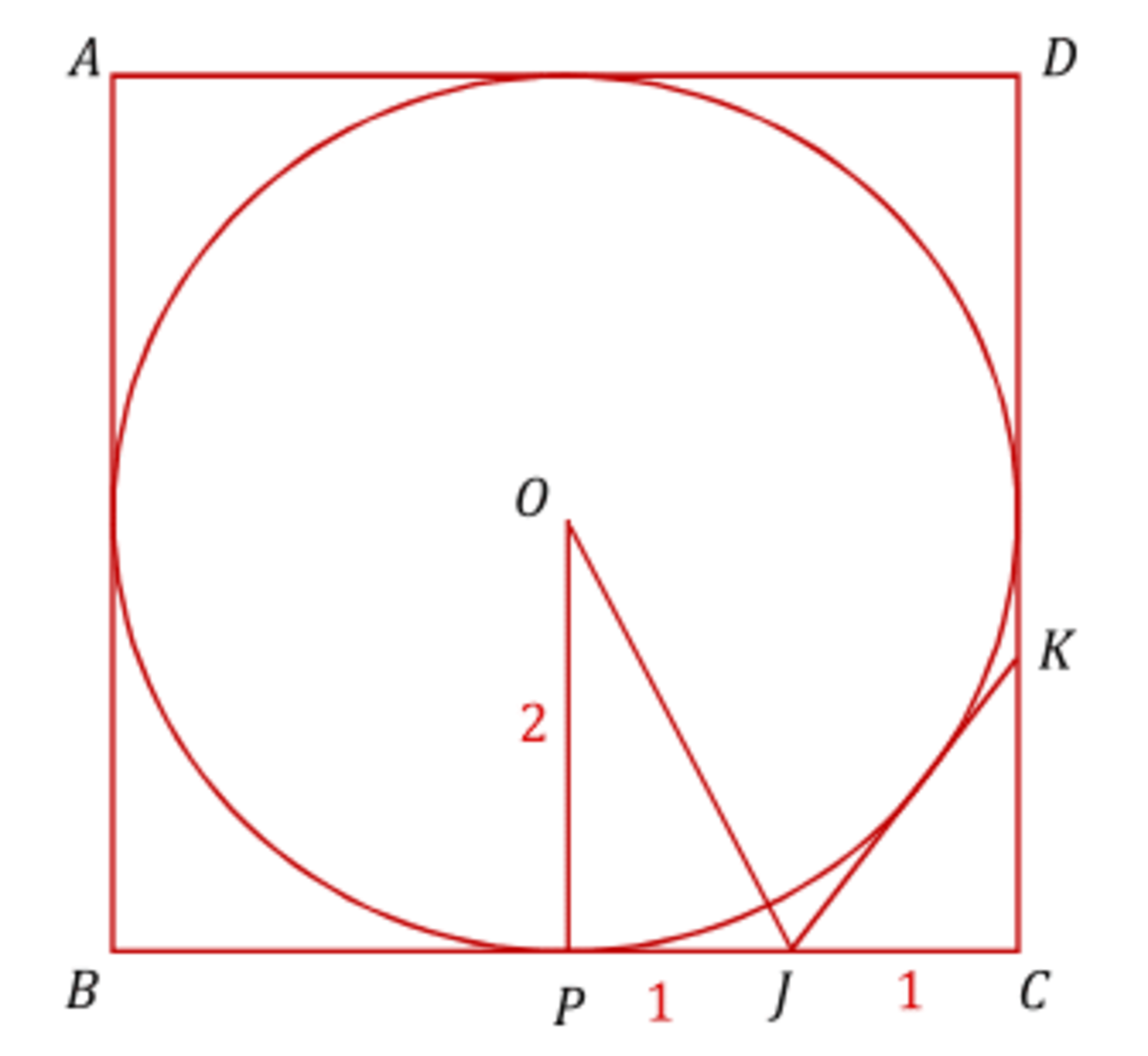
Let the centre of the circle be O , the point of tangency of the circle with B C be P . Without loss of generality, let O ( 0 , 0 ) , P ( 0 , − 1 ) , C ( 1 , − 1 ) . It becomes obvious that J ( 0 . 5 , − 1 ) . Now consider a line passing through J with gradient k . The line will have equation of the form y = k x − 0 . 5 k − 1 We equate this with the equation of the circle x 2 = y 2 = r 2 to obtain: x 2 + ( k x − 0 . 5 k − 1 ) 2 = 1 As the line must be tangent to the circle, the discriminant of this equation in x must also be 0 to ensure that there is only one point of intersection. Thus k = 3 4 . This results in K ( 1 , − 3 2 ) , yielding 3 as our desired answer.