Geometry problem 1 by Dhaval Furia
In △ A B C , medians A D and B E are perpendicular to each other, and have lengths 1 2 c m and 9 c m , respectively. Then what is the area of △ A B C , in s q c m ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
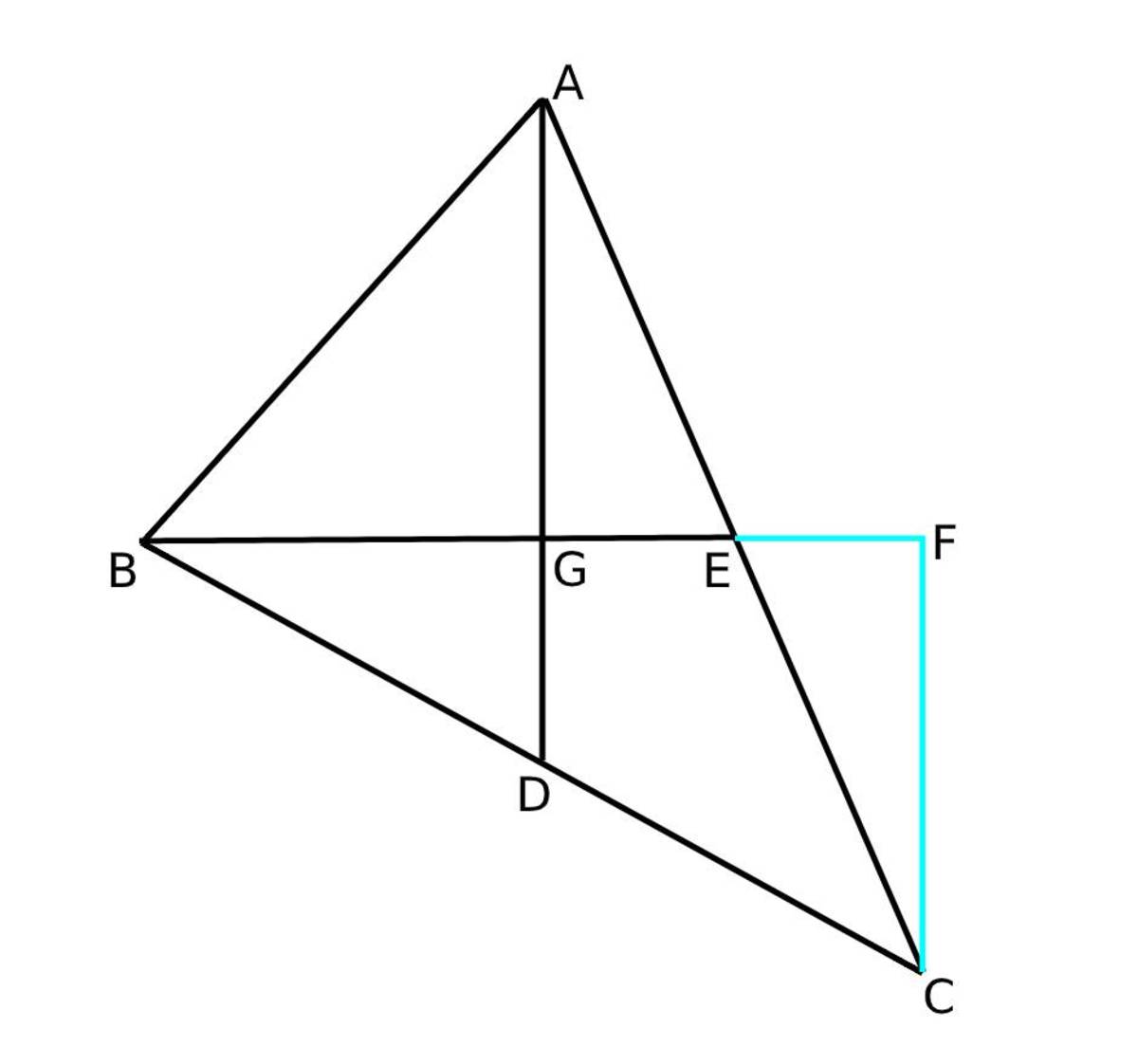
We have A D = 1 2 and B E = 9 . We know that intersections of medians divides the median in the ratio 2 : 1
So A G : G D = 2 : 1 and A G + G D = 1 2
⇒ A G = 8 and G D = 4
Draw C F ⊥ B E . Then in △ B C F , D is mid point of B C and D G ∥ C F . So △ B D G ∼ △ B C F
B C B D = 2 1 = C F G D
⇒ C F = 2 G D = 8
Now, area of △ A B C = area of △ A B E + area of △ B E C
⇒ ar ( △ A B C ) = 2 1 B E ⋅ A G + 2 1 B E ⋅ C F
⇒ ar ( △ A B C ) = 2 1 ⋅ 9 ⋅ 8 + 2 1 ⋅ 9 ⋅ 8
⇒ ar ( △ A B C ) = 3 6 + 3 6 = 7 2
The three medians of a triangle are concurrent. Let the intersection of the three medians be X . So
A X = 3 2 ( 1 2 ) = 8 c m
E X = 3 1 ( 9 ) = 3 c m
△ A X E is a right triangle and its area is
A △ A X E = 2 1 × 3 × 8 = 1 2 c m 2
The three medians together divide a triangle into six equal parts, so the area of △ A B C is
A △ A B C = 6 × 1 2 = 72 square centimeters