A geometry problem by Digi Verse
Geometry
Level
1
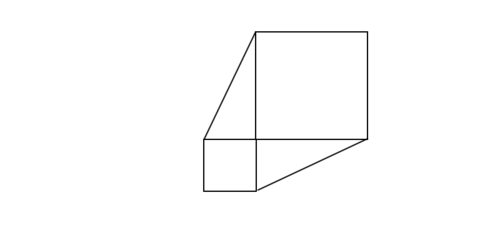There are two different sized squares with a common vertex. They meet at a right angle. Then, a line of length 9 is drawn between the two squares, as illustrated. What is the combined area of the two squares?
The answer is 81.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The line between them creates a right triangle, of which the hypothenuse has length 9. It is stated that the sum of the square of the two legs is equal to the square of the hypothenuse, which in this case, is 9. The square of the two legs would also be equal to the area of each square. Therefore, the sum of the area of the two squares would be 9^2, or 81.