Square Arrangement

b = 1 + g

g = f + 1

b = 2 + f

c = b + 1

c = 2 + f + 1

c = 3 + f

d = e + c

d = e + 3 + f

d = 3 + e + f

h = f + g

h = 2f + 1

i = e + d

i = 2e + 3 + f

vertical sides give d + c + b = i + h

subtituting values result to e = 4

horizontal sides give b + g + h = d + i

subtituting values result to f = 7

then

b = 9 ; c = 10 ; d = 14 ; g = 8 ; h = 15 ; i = 18

sides are 33 x 32

area = 1056

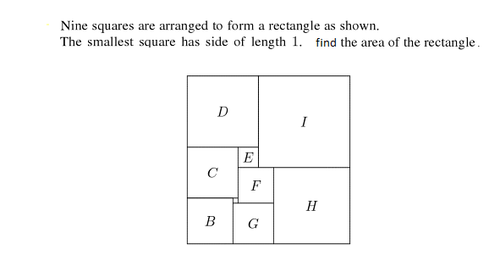
Start with the area around the smallest rectangle. We see immediately that (using small letters to denote length of the corresponding squares), $f+1 = g,$ $g + 1 = b,$ $1 + b = c,$ $1+c = e+ f.$ From these equations we can get $e = 4$ and $b = f + 2$ , $c = f + 3$ .

The picture also shows that $d = c + e = f + 7$ and $i = d + e = f + 11$ . Moreover $h = f + g = 2f + 1$ . Now the width of the rectangle can be expressed both as $d + i$ and as $b + g + h$ . Therefore it must hold that $f + 7 + f + 11 = f + 2 + f + 1 + 2f + 1,$ which implies that $f = 7$ . Plugging this back into other equations we get $i = 18$ , $h = 15$ and $d = 14$ . Therefore the width of the rectangle is $d + i = 32$ and its height is $i + h = 33$ and the resulting area turns out to be $32 \cdot 33 = {\bf 1056}$ .

G=f+1 ,B=f+2 ,C=f+3 = f-1+E then e=4 ,D=c+4 = f+7 ,H=f+f+1=2f+1 ,I=d+4 = f+11 then width of triangle = i+D = f+18 ....1 ,Also Width of triangle = b+g+h = 4f+4 ..... 2 ,From 1& 2 f= 7 ,Length = d+c+b=3f+12 ,Then width = 32 & length = 33 ,Then area of rectangle = 33x32 = 1056 #

Suppose side of square B is x.

B=x

C=B+side of smallest square =x+1

G=B-side of smallest square=x-1

F=G-side of smallest square=x-2

E=C+side of smallest square-F =>x+1+1-x+2 i.e E=4

D=C+E i.e D=x+5

I=D+E i.e I=x+9

H=I+E-F =>H=x+9+4-x+2 =>H=15

F+G=H =>x-1+x-2=15=>2x-3=15=>x=9

Side A of rectangle=B+G+H=x+x-1+15=2x+14=32

Side B of rectangle=I+H=x+9+15=33

Area of rectangle= 32*33=1056