Zig Zag Lines And Their Relationships
Find the value of x in term a , b , and c .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
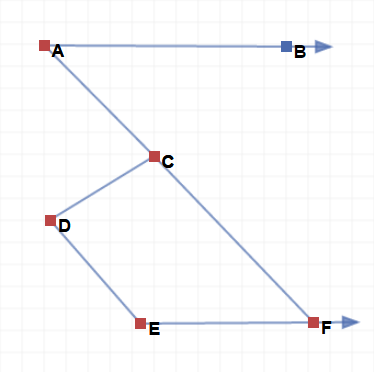
Our Original Figure is B A C D E F . Where ∠ B A C = x , ∠ A C D = a , ∠ C D E = b and ∠ D E F = c
Join Point C and Point F . From the Figure :
∠ B A C = ∠ C F E = x and ∠ D C F = 1 8 0 − a
In Quadrilateral C D E F :
x + 1 8 0 − a + b + c = 3 6 0
x = a − b − c + 1 8 0
Doesn't this solution assume that lines AB and EF are parallel? Nothing about the problem suggests this is the case. Or am I missing something?
@Sambhrant Sachan Nice solution
@Sambhrant Sachan Can you rate this problem?
@Jose Chavira The two arrows indicate that the lines are parallel
This is the solution I picked before submitting the answer.
@Sambhrant Sachan Thank you
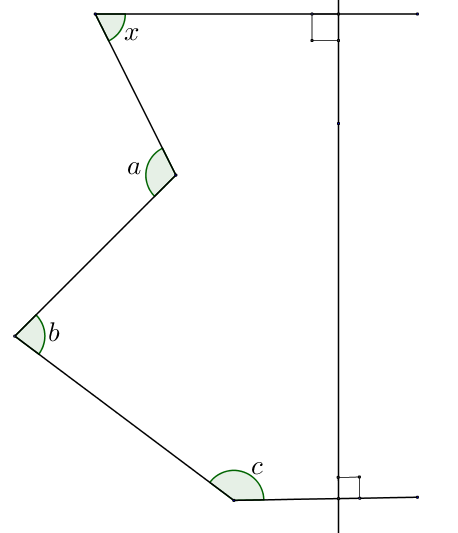
7 2 0 = x + ( 3 6 0 − a ) + b + c + 9 0 + 9 0
7 2 0 = x + 5 4 0 − a + b + c
1 8 0 + a − b − c = x
amazing that is the best method to apprehend this problem.
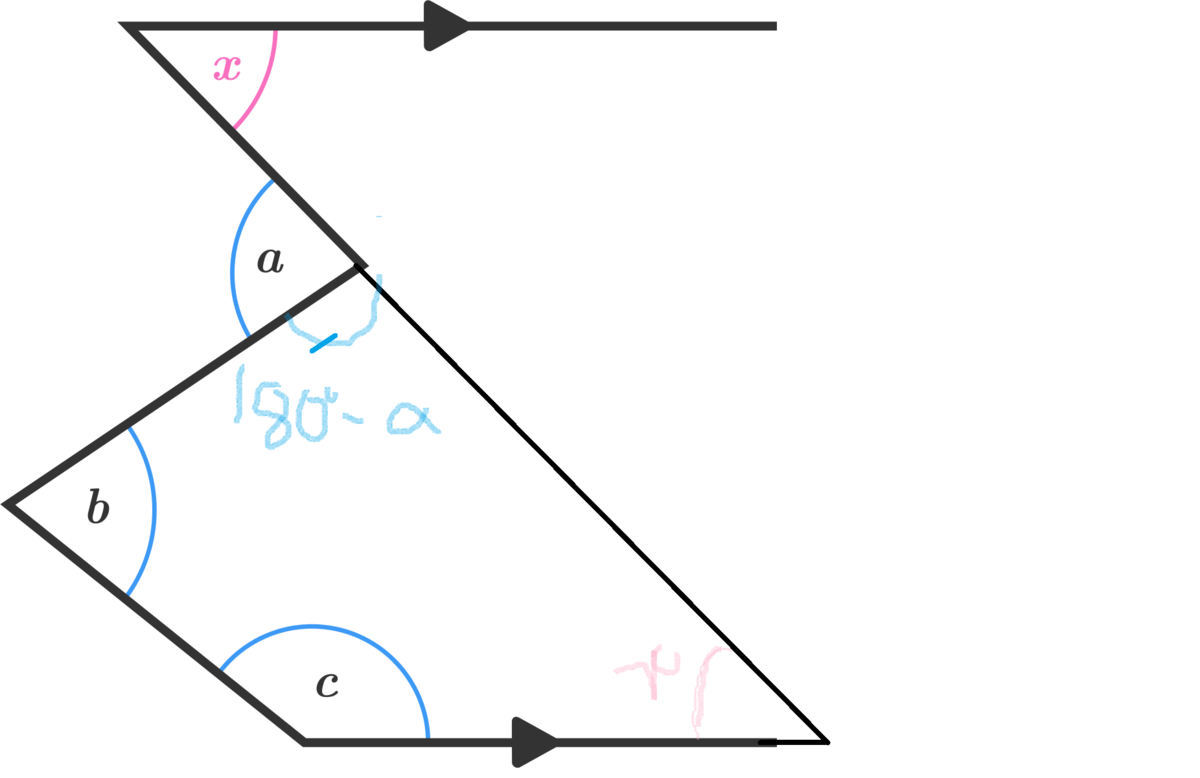
very simple solution from the figure :
since in the figure we have a quadrilateral and because sum of angles of quadrilateral is 3 6 0
= > x + b + c + 1 8 0 − a = 3 6 0 = = > x = 1 8 0 + a − b − c
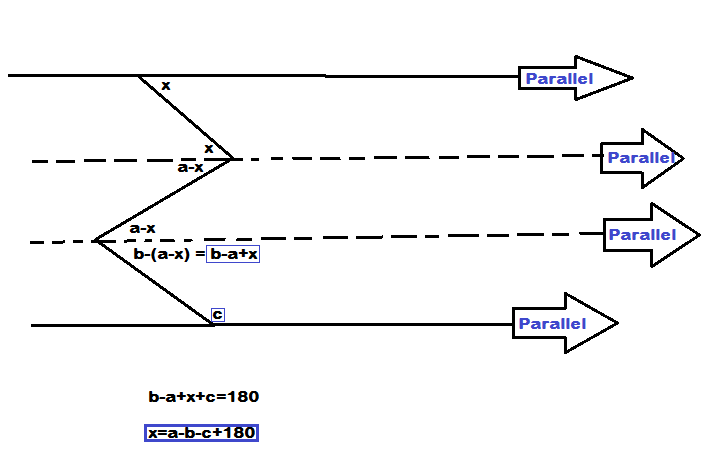
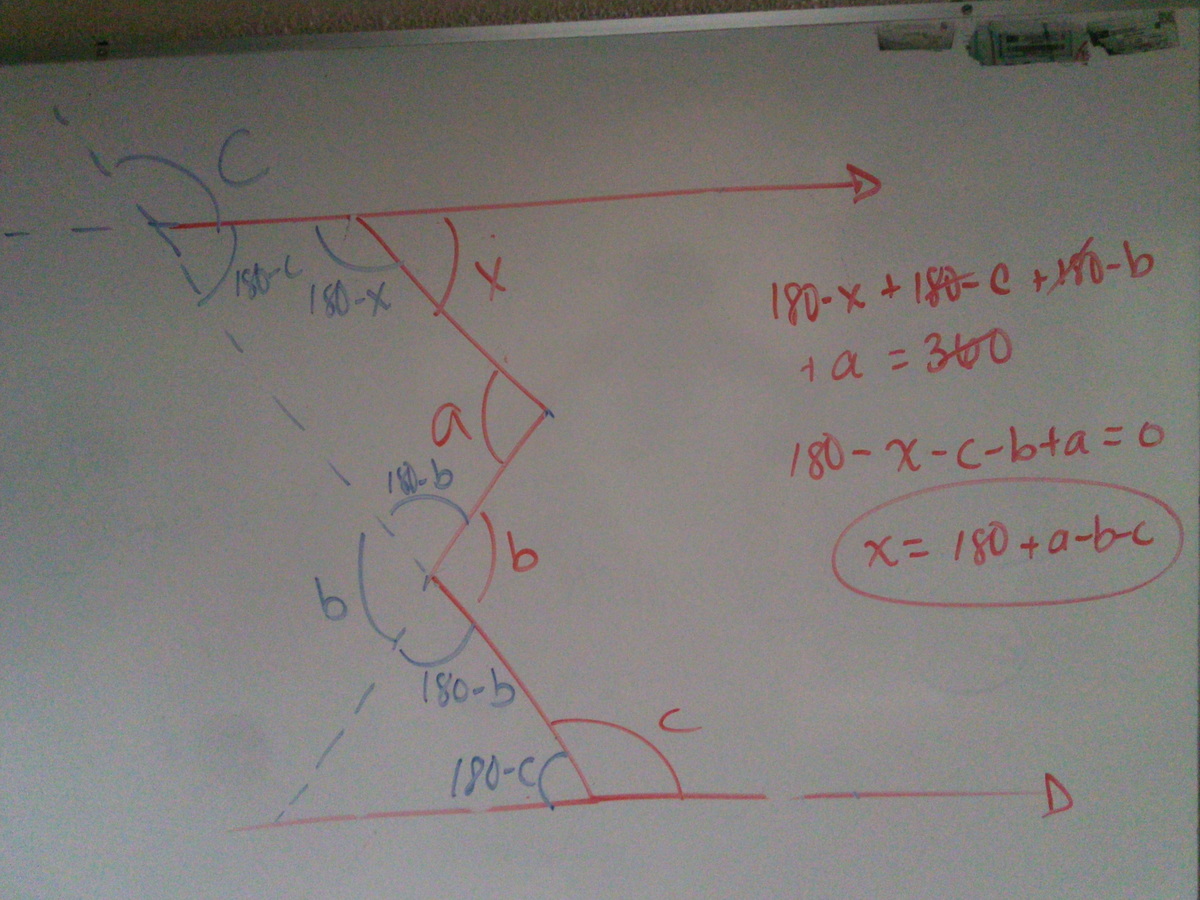
x = a − b − c + 1 8 0