A geometry problem by Filippo Olivetti

In Filippo's diagram, it isn't difficult to prove that BK=KR=2KO. Let KO=x; then AK=√(42²+x²) and (AK)(KB)=(42-x)(42+x) which gives us 2x√(42²+x²)=42²-x² yielding x=14√(6√3-9). Further, AH/AB=AO/AK which means:AH/(√(42²+x²)+ 2x)=42/√(42²+x²). Plug in the value of x and solve for AH to get AH=42√3 or AH²=5292.

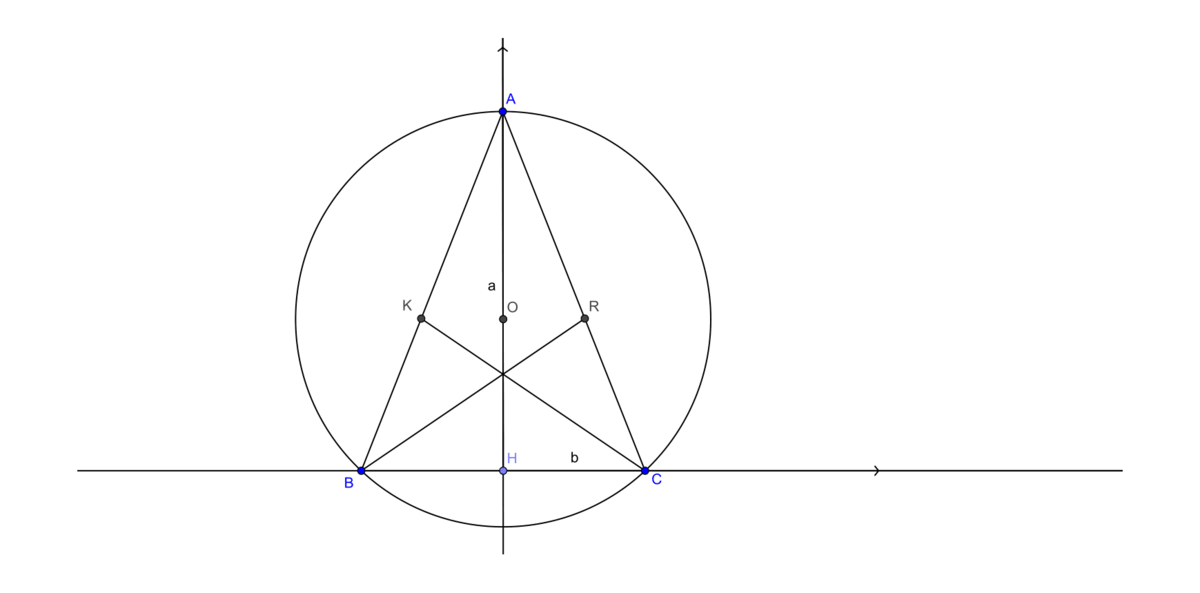
I'll use analytic geometry to solve this problem.

Let $AH = a$ and $CH = b$ , such that $A (0,a), C(b,0)$ . Using the Pythagorean theorem, we get: $(a-42)^2 + b^2 = 42^2$ since $OA = 42$ from hypothesis. Let $r_{AC}$ and $r_{AB}$ the lines that pass through $AC$ and $AB$ rispectively. Then $r_{AC} : ax +by -ab=0$ $r_{AB}: ax-by+ab=0$ The bisector is the locus of the points that are equidistant from two lines. So the bisector of $\angle ABC$ is: $\frac{ax-by+ab}{\sqrt{a^2+b^2}} = y$ In order to find $K$ , we put in a system the bisector and $r_{AC}$ : $\begin{cases} ax-by+ab= y \cdot \sqrt{a^2+b^2} \\ ax+by-ab=0\\ \end{cases}$ Solving the system we get: $y= \frac{2ab}{\sqrt{a^2+b^2}+2b}$ For symmetry, $R$ have the same ordinate; since $R,K,O$ are allineate from hypothesis $a-42= \frac{2ab}{\sqrt{a^2+b^2}+2b}$ Using the equation $(a-42)^2 + b^2 = 42^2$ we have found before, we get: $a^2 = \boxed{3 \cdot 42^2}$