A geometry problem by Filippo Olivetti

Geometry Level 4

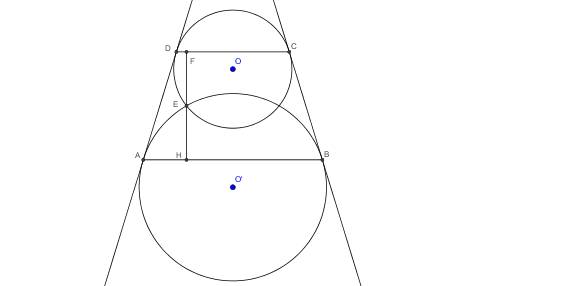
Let $ABCD$ be an isoscel trapezoid with $AB$ and $CD$ as bases, with $AB>CD$ . Let $\gamma$ be the circumference tangent to $BC$ and $AD$ , and with $AB$ as a chord. Then, let $\gamma '$ be another circumference tangent to $BC$ and $AD$ , and with $CD$ as a chord. Then, define $\gamma \cap \gamma ' \equiv E$ (one among the two points of intersection), $F$ and $H$ the proiection of $E$ to $CD$ and $AB$ respectively. Is it true that $EF = EH$ ?

False True Not enough information

2 solutions

Ahmad Saad
May 24, 2017

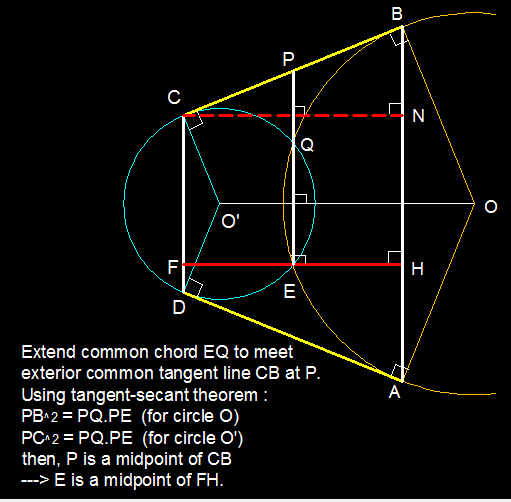
I also visualized by rotating the figure. Wow, you did just the same.

Prayas Rautray - 3 years, 10 months ago

Vishwash Kumar Γξω
May 25, 2017

$Sol^{\n}$ Let $G$ be the second point of intersection of $\gamma$ and $\gamma'.$ Let $K = EG \cap AB$ . Clearly, $K$ is on the radical axis $EG$ of the circles $\gamma$ and $\gamma'$ . Therefore, $Pow_\gamma (K)$ = $Pow_ \gamma' (K)$ $=> KA^{2} = DK^{2}$ => $KA$ $= DK$ . But since $DF || KE || AH$ , applying the theorem of intercepts in $DE , KE , AH$ and the trans. $FH$ and $DA$ , we get $FE = EH$ .

... Always $K.I.P.K.IG.$

What do you mean by pow(k???)

Prayas Rautray - 3 years, 10 months ago

A geometry problem by Filippo Olivetti

2 solutions

0 pending reports