A geometry problem by Francois Tardieu
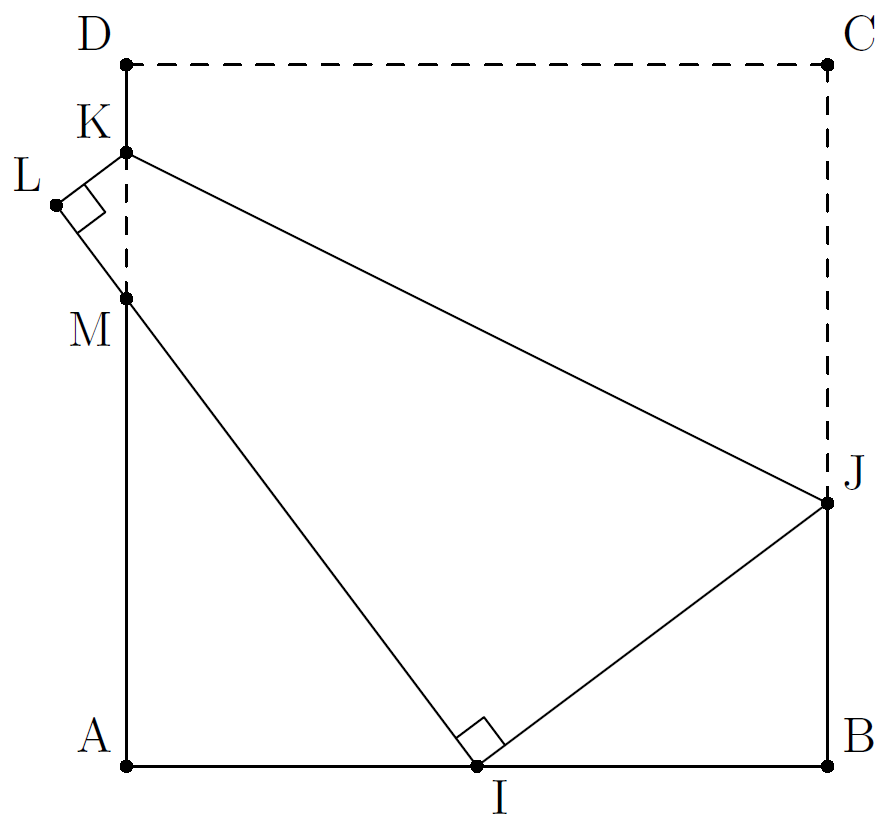
ABCD is a square paper. .
ABCD is folded so that point comes to middle point of segment .
Determine area of the quadrilateral IJKM.
The answer is 52.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We define: J C = x and J B = 1 2 − x so, I J = x and we have, A I = I B = 6
with Pythagoras in triangle IBJ
I J 2 = I B 2 + J B 2
⟺ x 2 = 6 2 + ( 1 2 − x ) 2 ⟺ x 2 = 3 6 + 1 4 4 − 2 4 x + x 2 ⟺ 2 4 x = 1 8 0 ⟺ x = 2 1 5 = 7 , 5
Then I J = x = 7 , 5 and J B = 1 2 − x = 4 , 5
we note, with the help of complimentary angles, that:
I J B = A I M = L K M (1)
and
B I J = A M I = L M K (2)
Let's say that: L M = y and L K = z so we get M I = 1 2 − y
and with help of (1)
cos A I M = cos I J B ⟺ I M I A = 1 2 − y 6 ⟺ 7 , 5 4 , 5 = 1 2 − y 6 ⟺ 3 ( 1 2 − y ) = 3 0 ⟺ y = 2
and with help of (2)
tan L M K = tan B I J ⟺ 2 z = 6 4 , 5 ⟺ z = 1 , 5
we can compute areas now:
area(IJKL) = 2 1 × ( L K + I J ) × L I = 2 1 × ( 1 , 5 + 7 , 5 ) × 1 2 = 5 4
area(LKM) = 2 1 × L K × L M = 2 1 × 1 , 5 × 2 = 1 , 5
area(IJKM)=area(IJKL) -area(LKM) = 5 4 − 1 , 5 = 5 2 , 5