A geometry problem by Miles Koumouris
What is the diameter of the semicircle in the diagram below?
Note: The diagram is not drawn to scale.
The answer is 112.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Nice Solution! But my approach : Applied Ptolemy and Pythagoras theorems. Say 'd' be the diameter... so by Ptolemy ( 58d + 7x92) = BD x AC and BD = {d^2 - (92)^2}^(1/2) & AC = {d^2 - 7^2}^(1/2) by solving it ... results the equation d^3 - 11877d - 74704 = 0
I don't understand how you can assume ABD is a right angle. How did you get to that conclusion?
Log in to reply
It is a theorem that the angle inscribed in a semicircle is always a right angle (90°) (check this link ).
Nice solution
Ugh, I was dancing around this idea, all I needed was to physically get the cosine of 180-theta... oh well. Very nice solution. Minor correction: the line before you multiply both sides by D to get the cubic formula, the right hand side you say "12544 + ...", isn't that suppose to be 11877?
How did you solve the third degree equation? I did not understand the factoration
Log in to reply
You can use rational root theorem to solve it. Refer to the link .
Brilliant ques and soln :P
Very nice solution. You are always the best. Salute
Brilliant !
Nice solution, though you are abusing the poor letter 'D'.
It got too messy, but the problem could be solved by applying the law of cosines by drawing radii to each vertex, forming three angles at the center of the circle. So 92^2 = r^2 + r^2 -2r^2cos(A),and similarly for the other two chords. You then get an equation like arcos(A) + arcos(B) + arcos(c) = 180, where A,B, and C are functions of r^2. Then that equation can be solved iteratively by a Newton-Raphson technique, but the solution presented is much more elegant. Ed Gray
-
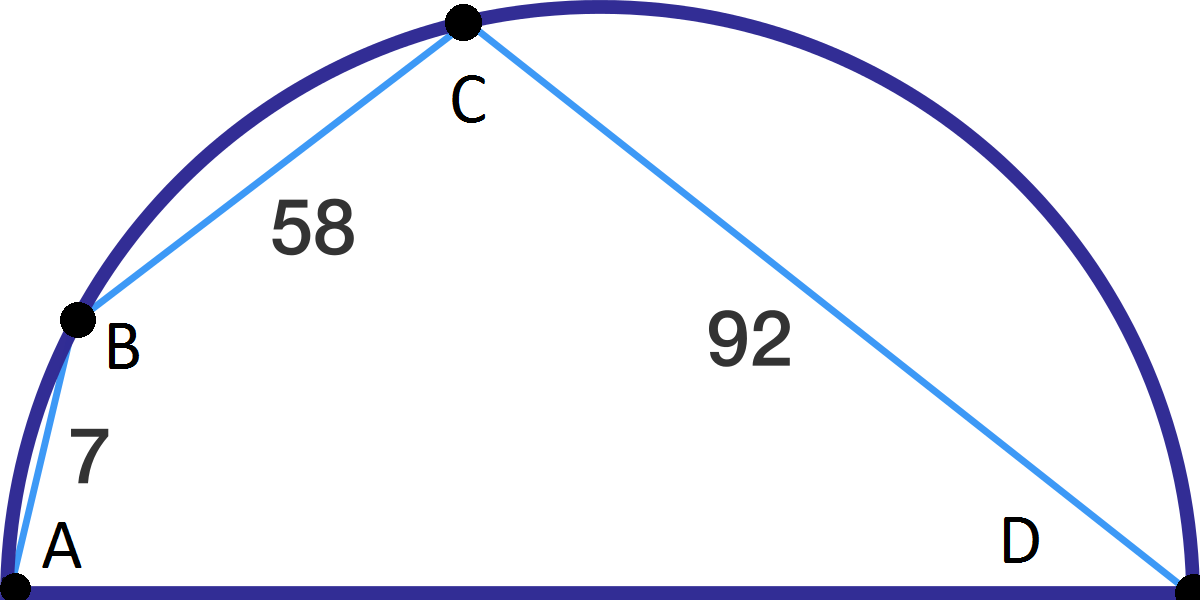 Let the diameter of the semicircle be of length x. Since the quadrilateral is cyclic (It can be inscribed in a circle), by Ptolemy's Theorem,
5
8
x
+
9
2
⋅
7
=
A
C
⋅
B
D
.
Notice that the diagonals
A
C
and
B
D
form right triangles with the diameter, therefore, we can rewrite
A
C
as
x
2
−
9
2
2
and
B
D
as
x
2
−
7
2
.
Replacing these into the equation gets us
5
8
x
+
9
2
⋅
7
=
(
x
2
−
9
2
2
)
⋅
(
x
2
−
7
2
)
.
Squaring both sides gets us
3
3
6
4
x
2
+
7
4
7
0
4
x
+
4
1
4
7
3
6
=
(
x
2
−
9
2
2
)
(
x
2
−
7
2
)
. From here, we solve for x.
3
3
6
4
x
2
+
7
4
7
0
4
x
+
4
1
4
7
3
6
=
x
4
−
8
5
1
3
x
2
+
4
1
4
7
3
6
x
4
−
1
1
8
7
7
x
2
−
7
4
7
0
4
x
=
0
x
3
−
1
1
8
7
7
x
−
7
4
7
0
4
=
0
(
x
−
1
1
2
)
(
x
2
+
1
1
2
x
+
6
6
7
)
=
0
⟹
x
=
1
1
2
Let the diameter of the semicircle be of length x. Since the quadrilateral is cyclic (It can be inscribed in a circle), by Ptolemy's Theorem,
5
8
x
+
9
2
⋅
7
=
A
C
⋅
B
D
.
Notice that the diagonals
A
C
and
B
D
form right triangles with the diameter, therefore, we can rewrite
A
C
as
x
2
−
9
2
2
and
B
D
as
x
2
−
7
2
.
Replacing these into the equation gets us
5
8
x
+
9
2
⋅
7
=
(
x
2
−
9
2
2
)
⋅
(
x
2
−
7
2
)
.
Squaring both sides gets us
3
3
6
4
x
2
+
7
4
7
0
4
x
+
4
1
4
7
3
6
=
(
x
2
−
9
2
2
)
(
x
2
−
7
2
)
. From here, we solve for x.
3
3
6
4
x
2
+
7
4
7
0
4
x
+
4
1
4
7
3
6
=
x
4
−
8
5
1
3
x
2
+
4
1
4
7
3
6
x
4
−
1
1
8
7
7
x
2
−
7
4
7
0
4
x
=
0
x
3
−
1
1
8
7
7
x
−
7
4
7
0
4
=
0
(
x
−
1
1
2
)
(
x
2
+
1
1
2
x
+
6
6
7
)
=
0
⟹
x
=
1
1
2
How do you know for sure that they make right angles?
Log in to reply
have you forgotten the properties of a circle? It's my approbation read again....:P
Wow. How did you think of that?
I love this solution since it doesn't even require trigonometry.
same solution here :)
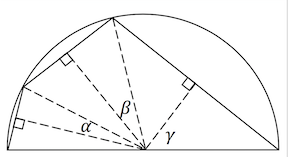
Let the radius of the semicircle be r . From the diagram, it is evident that
sin ( α ) = 2 r 7
sin ( β ) = r 2 9
sin ( γ ) = r 4 6 .
Since it is known that 2 α + 2 β + 2 γ = 1 8 0 ∘ ⟺ γ = 9 0 ∘ − ( α + β ) , we can say
sin ( γ ) = cos ( α + β )
cos ( α + β ) = cos ( α ) cos ( β ) − sin ( α ) sin ( β ) (by angle addition identities).
Letting sin ( α ) = 2 r 7 = x , it is evident from trigonometric identites that
cos ( α + β ) = ( 1 − x 2 ) ( 1 − ( 7 5 8 x ) 2 ) − 7 5 8 x 2 = 7 9 2 x
( 7 2 + 5 8 2 + 9 2 2 ) x 2 + ( 2 × 5 8 × 9 2 ) x 3 − 7 2 = 0 .
Substituting x back as 2 r 7 gives
4 r 3 − ( 7 2 + 5 8 2 + 9 2 2 ) r − ( 7 × 5 8 × 9 2 ) = 0
( r − 5 6 ) ( 4 r 2 + 2 2 4 r + 6 6 7 ) = 0 .
So r = 5 6 , and thus the diameter of the semicircle is 1 1 2 .
This solution has the advantage to be universal : no need to know cyclic quadrilaterals, nor to prove their properties.
use ptolemy's equality then ( D 2 − 9 2 2 ) ( D 2 − 7 2 ) = 5 8 D − 9 2 ∗ 7 = 5 8 D + 6 4 4 then square both side then simplifying we get D 3 − 1 1 8 7 7 D − 7 4 7 0 4 = 0 , then solve it by factorization D = 1 1 2 :)
Let p and q be the shorter and longer diagonals of the quadrilateral and d be the diameter of the semicircle. By Pythagorean and Ptolemy theorems,
p 2 + 9 2 2 = d 2 = 7 2 + q 2 and p q = 5 8 d + 7 ⋅ 9 2 , ( 5 8 d + 7 ⋅ 9 2 ) 2 = ( p q ) 2 = ( d 2 − 9 2 2 ) ( d 2 − 7 2 ) , d 4 − ( 9 2 2 + 7 2 + 5 8 2 ) d 2 − ( 2 ⋅ 5 8 ⋅ 7 ⋅ 9 2 ) d = 0 , ( d − 1 1 2 ) ( d 2 + 1 1 2 d + 6 6 7 ) = 0 , d = 1 1 2 or ( d + 5 6 ) 2 = 2 4 6 9 < 5 0 2 , But d > 0, so d = 1 1 2 .
Let the diameter of the semicircle be D and ∠ B C D = θ . For a cyclic quadrilateral A B C D , ∠ B A D = 1 8 0 ∘ − θ .
Using cosine rule on △ B C D :
B D 2 D 2 − 7 2 D 2 − 4 9 D 2 = B C 2 + C D 2 − 2 B C ⋅ C D cos θ = 5 8 2 + 9 2 2 − 2 ( 5 8 ) ( 9 2 ) cos θ = 3 3 6 4 + 8 4 6 4 − 1 0 6 7 2 ( − D 7 ) = 1 1 8 7 7 + D 7 4 7 0 7 By Pythagorean theorem: B D 2 = A D 2 − A B 2 As cos ( 1 8 0 ∘ − θ ) = D 7 , cos θ = − D 7
⟹ D 3 − 1 1 8 7 7 D − 7 4 7 0 4 ( D − 1 1 2 ) ( D 2 + 1 1 2 D + 6 6 7 ) ⟹ D = 0 = 0 = 1 1 2 D 2 + 1 1 2 D + 6 6 7 gives negative roots