A geometry problem by Guntitat Sawadwuthikul

Geometry Level 3

ABC is a right triangle, with the length of x , y x, y and z z , with z z represents the hypotenuse. If the height of the triangle equals to 8, having z z as the base. Find the value of ( x + 8 ) ( y + 8 ) ( x − 8 ) ( y − 8 ) (x+8)(y+8)(x-8)(y-8) .


The answer is 4096.

Guntitat Sawadwuthikul by Guntitat Sawadwuthikul , 20, Thailand

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

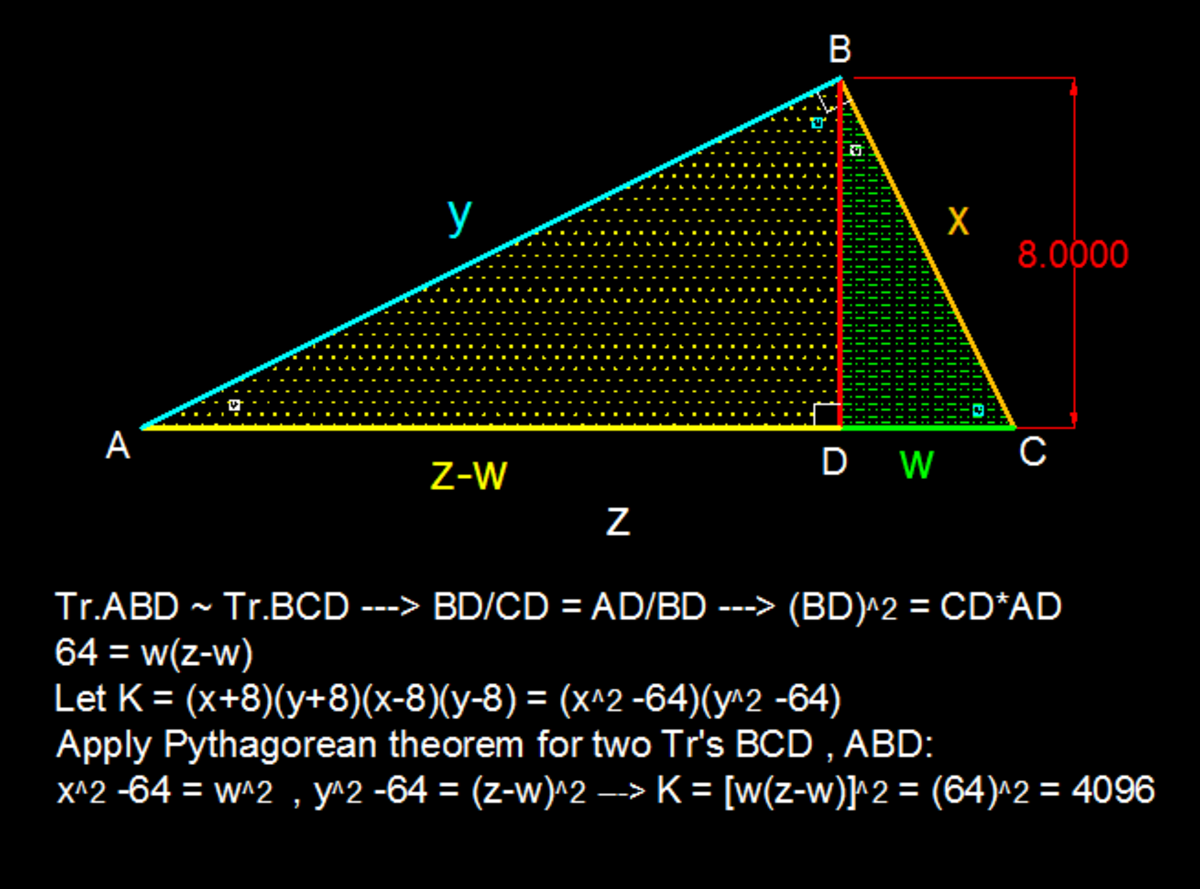
As Δ A B C \Delta ABC is right angled we know that x 2 + y 2 = z 2 x^{2} + y^{2} = z^{2} and x y = 8 z xy = 8z . So

( x + 8 ) ( y + 8 ) ( x − 8 ) ( y − 8 ) = ( x 2 − 64 ) ( y 2 − 64 ) = (x + 8)(y + 8)(x - 8)(y - 8) = (x^{2} - 64)(y^{2} - 64) =

( x y ) 2 − 64 ( x 2 + y 2 ) + 6 4 2 = ( 8 z ) 2 − 64 z 2 + 4096 = 4096 (xy)^{2} - 64(x^{2} + y^{2}) + 64^{2} = (8z)^{2} - 64z^{2} + 4096 = \boxed{4096} .

5 Helpful 0 Interesting 0 Brilliant 0 Confused
Ahmad Saad
Dec 16, 2016

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...