A geometry problem by Hana Wehbi
A
B
C
D
E
F
is a regular hexagon with
G
as the midpoint of
A
F
and
H
as the midpoint of
C
D
. What fraction of the hexagon is the red area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The same way l solved it. Thank you for a nice solution but also there is a long solution but l prefer this one, why make things complicated.
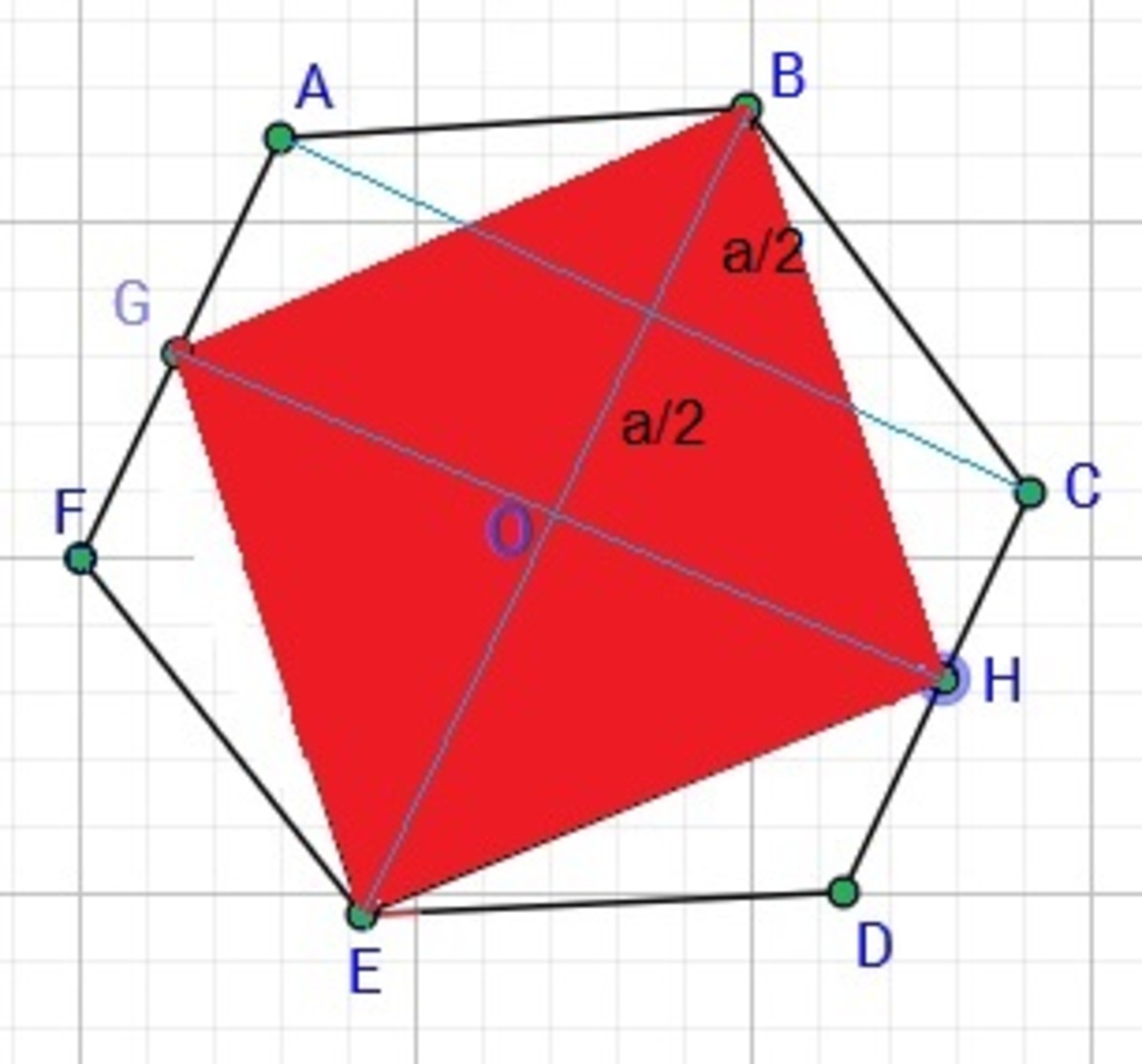Let the center of the regular hexagon be
O
,
B
O
=
a
and
A
C
=
G
H
=
b
. Note that
a
is also side length of the regular hexagon. We note that:
[ A B C D E F ] [ B H E G ] = [ A B C H G ] [ B H G ] = [ A C H G ] + [ A B C ] 2 1 a b = 2 1 a b + 2 1 × 2 a × b 2 1 a b = 4 3 2 1 = 3 2
Thank you for sharing a nice solution. I like your solution. it didn't come to my mind.
Since the purple lines are medians, [ E F G ] = [ A G B ] = [ B C H ] = [ H D E ] = t Since the hexagon is regular, by symmetry it is clear, that [ A B C D E F ] = 1 2 t From that the fraction is: 1 2 t 1 2 t − 4 t = 1 2 t 8 t = 3 t 2 t = 3 2