A geometry problem by Hana Wehbi
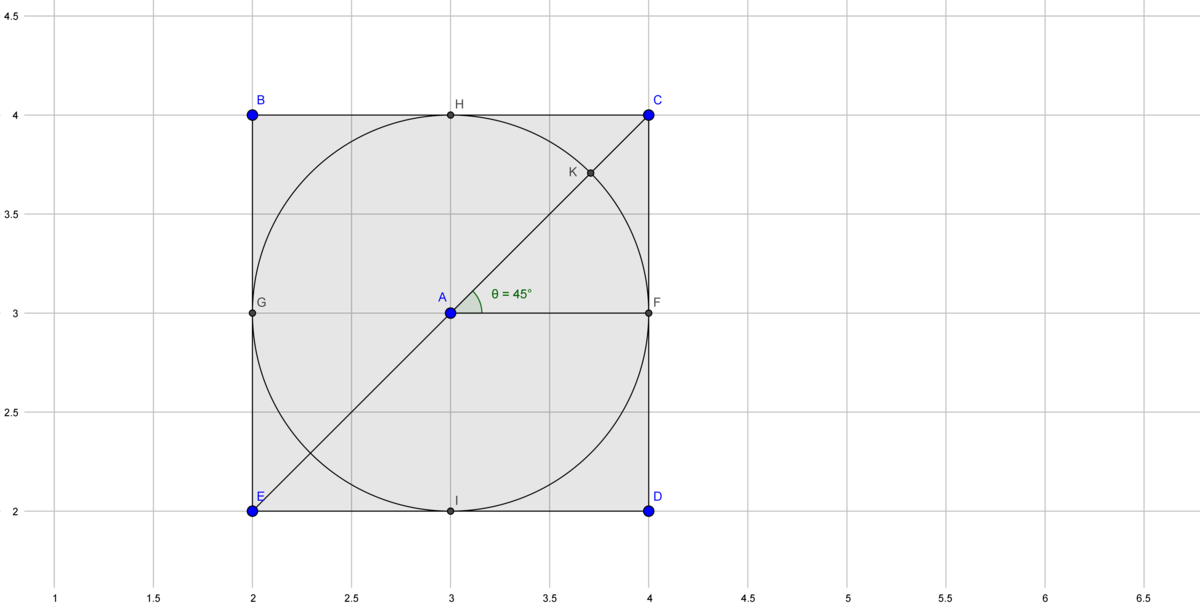
A circle is inscribed in a square as shown. The width of the square is the same as the diameter of the circle.
In the above diagram, approximately what percentage of the diagonal is outside the circle?( Rounded to the nearest tenth)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 A
F
=
A
K
=
r
(radius of the circle) &
θ
=
4
5
A
F
=
A
K
=
r
(radius of the circle) &
θ
=
4
5
s i n ( θ ) = 2 1 = A C F C = r + K C r
Solving for K C we get K C = ( 2 − 1 ) r
To answer the question "Approximately what percentage of the diagonal is outside the circle?", we have to find A C K C
A C K C = r + ( 2 − 1 ) r ( 2 − 1 ) r = 1 − 2 1 = ~ 0 . 2 9 3 So the answer is 2 9 . 3 %
Thank you.
Thank you very much
An easy way to solve this is to take numerical values. Suppose the side of the square is 2 which is the same as the diameter of the circle. Thus by using Pythagoras's theorem, the diagonal of the square measures 2 2 + 2 2 = 8 . Thus, the percentage of the diagonal that is outside the circle is 8 8 − 2 = 2 9 . 3 %