A Geometry Problem by Haosen Chen

$BD=BE, CF=CG, AD=AG=EF=30, \angle DIG=180, \angle DFG = \angle DEG=90, AF \parallel DE, AE \parallel GF$ .

It can be shown that point $H$ is an orthocentre of a triangle $AEF$ and that $\angle EAF = 45$ . For any triangle $ABC$ , $AH = \dfrac{BC}{\tan(A)}$ . In our case $AH = \dfrac{EF}{\tan(45)} = 30$ .

For more info on orthocentre property mentioned see my note .

Let $\omega$ be the incircle of $\Delta ABC$ such that $A', B',$ and $C'$ are the intersections on $BC, AC,$ and $AB$ respectively. Let $r$ denote the radius of the incircle and $R$ the radius of the larger circle. Let $EH = x$ and $HF= y$ .

To solve for $r$ , notice that $\Delta ABC = sr$ , where $s=\dfrac{a+b+c}{2}$ , so $r = 15.$

Notice that $AC' = DC' = AB' = GB' = r$ . So $DG = 2r\sqrt{2}$ and $R = r\sqrt{2}$ . Also $\angle ADG = \angle AGD = 45^{\circ}.$

Since $\Delta DGH \sim \Delta EFH, DH=EH\sqrt{2}=x\sqrt{2}$ and $GH=HF\sqrt{2}=y\sqrt{2}.$

Notice that $D-I-G$ is collinear since $\angle BCA = 90^{\circ} = \angle DEG = \angle DFG$ and by Converse of Thales Theorem.

Also $DG=BE$ and $CG=CF$ since $DC' = EA' = GB' = FA' = r.$

By law of cosines, we obtain $\angle ABC = \cos^{-1}({\frac{55}{73}})$ and $\angle ACB = 90 - \cos^{-1}({\frac{55}{73}})$

After a series of angle chasing, $\angle GDF = \frac{\cos^{-1}({\frac{55}{73}})}{2}.$ So $\angle ADH = 45 + \frac{\cos^{-1}({\frac{55}{73}})}{2}$ .

By law of cosines and then pythagorean, $1800 = 1250(\frac{55}{73}) + (x\sqrt{2} + y)^2 ; 1800 = 648(\frac{48}{73}) + (x + y\sqrt{2})^2.$ So $DH = 150\sqrt{\dfrac{2}{73}}.$

By law of cosines, $AH^2 = 30^2 + (150\sqrt{\frac{2}{73}})^2 - 2(30)(150\sqrt{\frac{2}{73})}\cos{(45 + \frac{\cos^{-1}({\dfrac{55}{73}})}{2})}$

$AH^2 = 30^2 + (22500)(\frac{2}{73}) - 2(30)(150\sqrt{\frac{2}{73}})(\dfrac{5}{2} \sqrt{\frac{2}{73}})$ .

$AH^2 = 30^2$

$AH = \boxed{30}.$

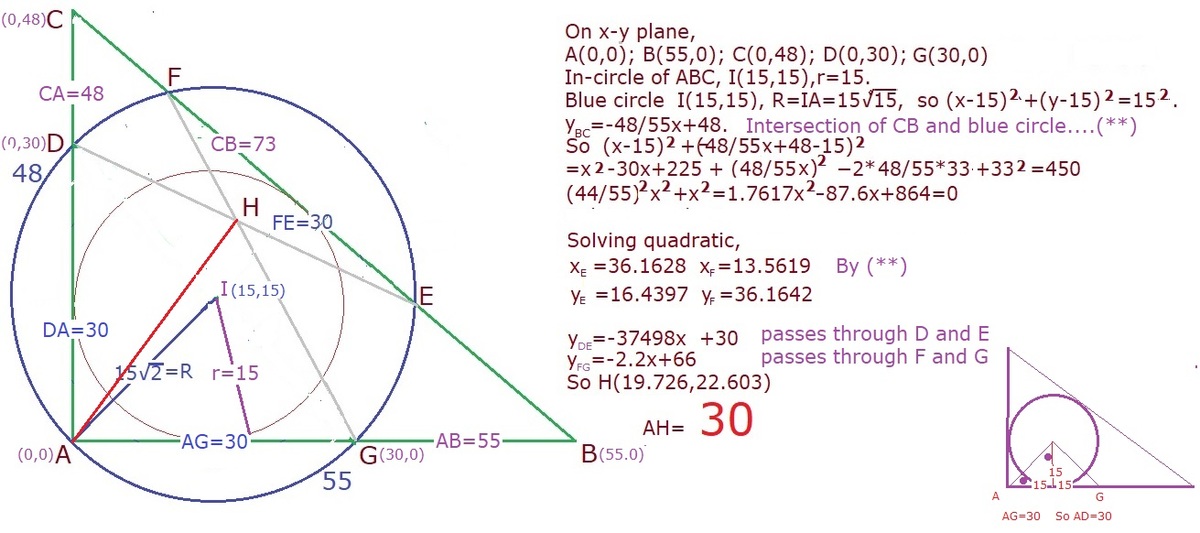
In triangle ABC we first find r and locate 'I'. Then draw the circle I(15,15), R= $15\sqrt2$ . As can be seen from the small sketch, we can locate D and G.
We calculate E and F coordinates through Intersection of blue circle and BC. Find equations of DE and FG.
Locate H, intersection of DE and FG.
Finally Distance of H from A(0,0).