A geometry problem by Harrison Froats
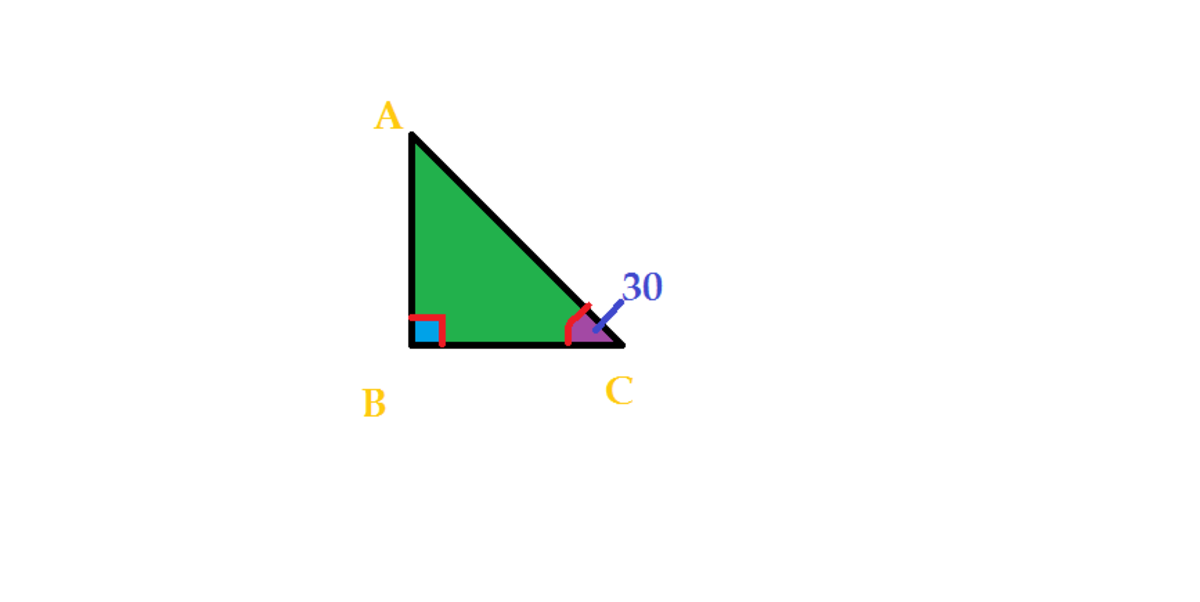
A right angle triangle has a hypotenuse that is 10.5cm long, and one of the angles is 30 degrees. Find the two other side lengths.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
=sin(30)\(\frac{opp}{10.5} )
o p p = s i n ( 3 0 ) x 1 0 . 5
o p p = 5 . 2 5 c m
= 1 0 . 5 2 − 5 . 2 5 2
= / s q r t [ 2 ] 8 2 . 6 8
= 9 . 0 9
 H
e
r
e
,
A
C
=
1
0
.
5
A
l
s
o
,
∠
C
=
3
0
∘
⟹
sin
3
0
=
2
1
⟹
A
C
A
B
=
2
1
⟹
1
0
.
5
A
B
=
2
1
∴
A
B
=
5
.
2
5
N
o
w
,
cos
3
0
=
2
3
A
C
B
C
=
2
3
1
0
.
5
B
C
=
2
3
⟹
B
C
=
5
.
2
5
3
≈
9
.
0
9
H
e
r
e
,
A
C
=
1
0
.
5
A
l
s
o
,
∠
C
=
3
0
∘
⟹
sin
3
0
=
2
1
⟹
A
C
A
B
=
2
1
⟹
1
0
.
5
A
B
=
2
1
∴
A
B
=
5
.
2
5
N
o
w
,
cos
3
0
=
2
3
A
C
B
C
=
2
3
1
0
.
5
B
C
=
2
3
⟹
B
C
=
5
.
2
5
3
≈
9
.
0
9
Given that we have 1 side length (10.5cm) and 2 angles (30° and 90°), we can use sine law.
s i n A a = s i n B b
a = s i n ( 3 0 ° ) × s i n ( 9 0 ° ) 1 0 . 5 c m
a = 5 . 2 5 c m
There is only one answer that has 5.25cm as a side length, therefore we don't have to solve for the other side length as it is the only option.
I used the 30-60-90 triangles with factor 10.5. This means the other sides are 10.5 * 0.5 and 40 * 0.5 * sqrt(3).