Partitioned Areas
A right triangle is divided into six smaller triangles by lines drawn from the vertices through a common interior point named as .
These lines which are drawn from vertices meet at points , respectively.
The areas of triangles are 84,35,30 and 40, respectively.
What is the area of triangle ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
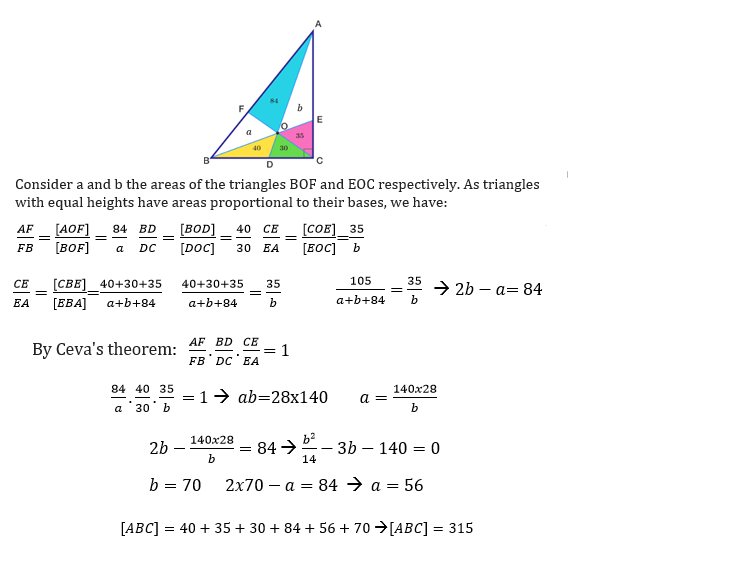
We will use the fact that for triangles with the same height (or base), the ratio of their areas is the ratio of their base (or height).
first ratio: [ B O F ] [ A O F ] = B F A F = [ B C F ] [ A C F ]
y 8 4 = y + 4 0 + 3 0 8 4 + x + 3 5
y 8 4 = y + 7 0 1 1 9 + x (this is our equation 1)
second ratio: [ C O E ] [ A O E ] = C E A E = C B E ] [ A B E ]
3 5 x = 4 0 + 3 0 + 3 5 x + y + 8 4 ⇒ 3 5 x = 1 0 5 x + y + 8 4
x = 0 . 5 y + 4 2 (this is our equation 2)
Solving the system of equations by substituting equation 2 into equation 1,
y 8 4 = y + 7 0 1 1 9 + 0 . 5 y + 4 2
0 . 5 y 2 + 7 7 y − 5 8 8 0 = 0
y = 5 6
x = 0 . 5 y + 4 2 = 7 0
Thus, the total area is 8 4 + 5 6 + 7 0 + 4 0 + 3 0 + 3 5 = 3 1 5