A geometry problem by Hosam Hajjir

Since $AB$ and $CD$ are on opposite faces of the cube and on the same plane, they are parallel, and by the same argument so are $AD$ and $BC$ . Therefore, $ABCD$ is a parallelogram.

The average height of the truncated cube would be the height at the centroid of this parallelogram, and since the centroid of a parallelogram is the midpoint of one of its diagonals, this height can be calculated by finding the average of the heights at $A$ and $C$ , which is $\frac{0 + 12}{2} = 6$ .

Therefore, the volume of the truncated cube is $V = 24 \cdot 24 \cdot 6 = \boxed{3456}$ .

Let side length $L$ be equal to $24$ . Let point $A$ be the origin.

Plane normal vector and plane equation:

$\vec{N} = (24,0,7) \times (24,24,12) = (-168,-120,576) \\ N_x \, x + N_y \, y + N_z \, z = 0 \\ z = -\frac{N_x}{N_z} \, x - \frac{N_y}{N_z} \, y = \alpha \, x + \beta \, y$

Volume under cutting plane:

$V = \int_0^L \int_0^L z \, dx \, dy = \int_0^L \int_0^L (\alpha \, x + \beta \, y) \, dx \, dy = \frac{L^3}{2} (\alpha + \beta) = \boxed{3456}$

The red solid is bounded by a plane ( $\pi$ parallel to the base of the cube at a height $12$ above it, and the cutting plane $ABCD$ .

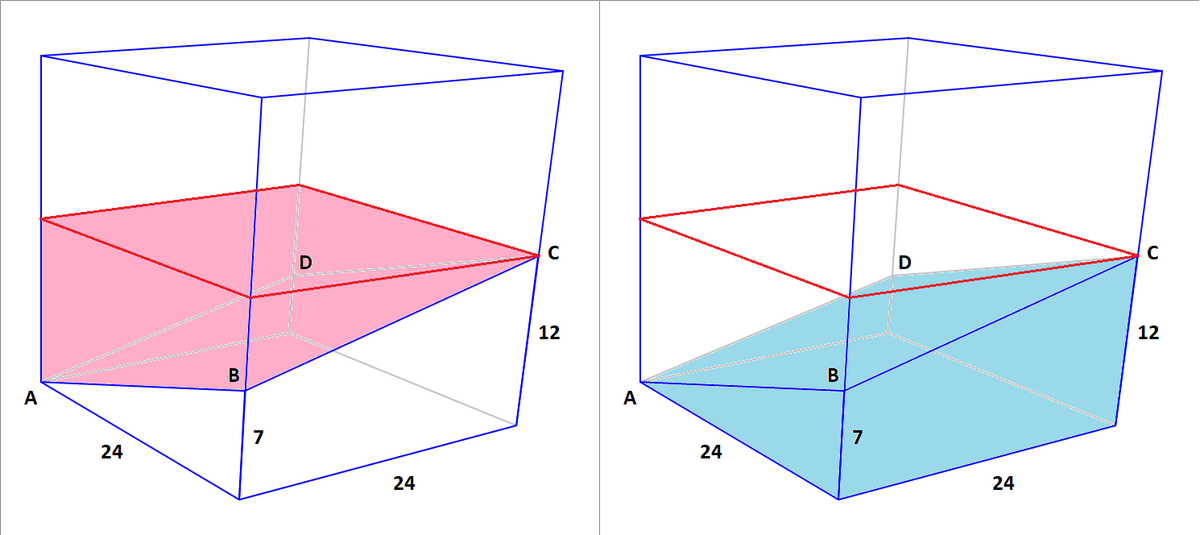
The volume of the blue solid is equal to the volume of the red solid; joined together they form a cuboid of dimensions $24\times 24\times 12$ , so the answer is $V=\frac{24\cdot24\cdot12}{2}=\boxed{3456}$

To convince yourself that the volumes are the same, note that point $D$ is at height $5$ above the base of the cube. This can be proved by considering the equation of the plane $ABCD$ , or just by noting that the lines $AC$ and $BD$ intersect at their midpoints at the centre of $ABCD$ .

It follows that point $A$ is $12$ below $\pi$ , point $B$ is $5$ below it, point $C$ is on $\pi$ , and point $D$ is $7$ below it - ie the red solid has exactly the same measures and angles as the blue solid, so they do indeed have the same volume. (They are mirror images of each other)

z = ax + by, origin at A. When x =24, y = 0, z = 7. When x = 24, y = 24, z =12, so a = 7/24, b = 5/24, V = integral from 0 to 24, integral from 0 to 24 of z= 7/24x + 5/24Y = 3456.