A geometry problem by Israel Sapnu Jr.

Geometry Level 2

If the length of the common chord intersecting circles is 16 and the radii are 10 and 17, find the distance between the two centers of the circle.


The answer is 21.

Israel Sapnu Jr. by Israel Sapnu Jr. , 35, Philippines

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

The distance between the two centers of the circles is given by:

1 0 2 − 8 2 + 1 7 2 − 8 2 = 6 + 15 = 21 \sqrt{10^2-8^2}+\sqrt{17^2-8^2} = 6+15 = \boxed{21}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

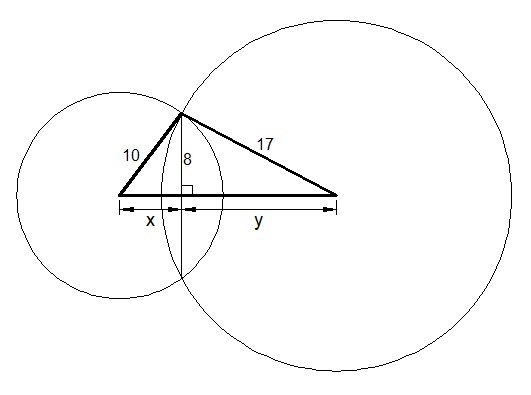Consider the figure on the left. The distance between the centers is

x + y = 1 0 2 − 8 2 + 1 7 2 − 8 2 = 6 + 15 = x+y=\sqrt{10^2-8^2}+\sqrt{17^2-8^2}=6+15= 21 \boxed{21}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...