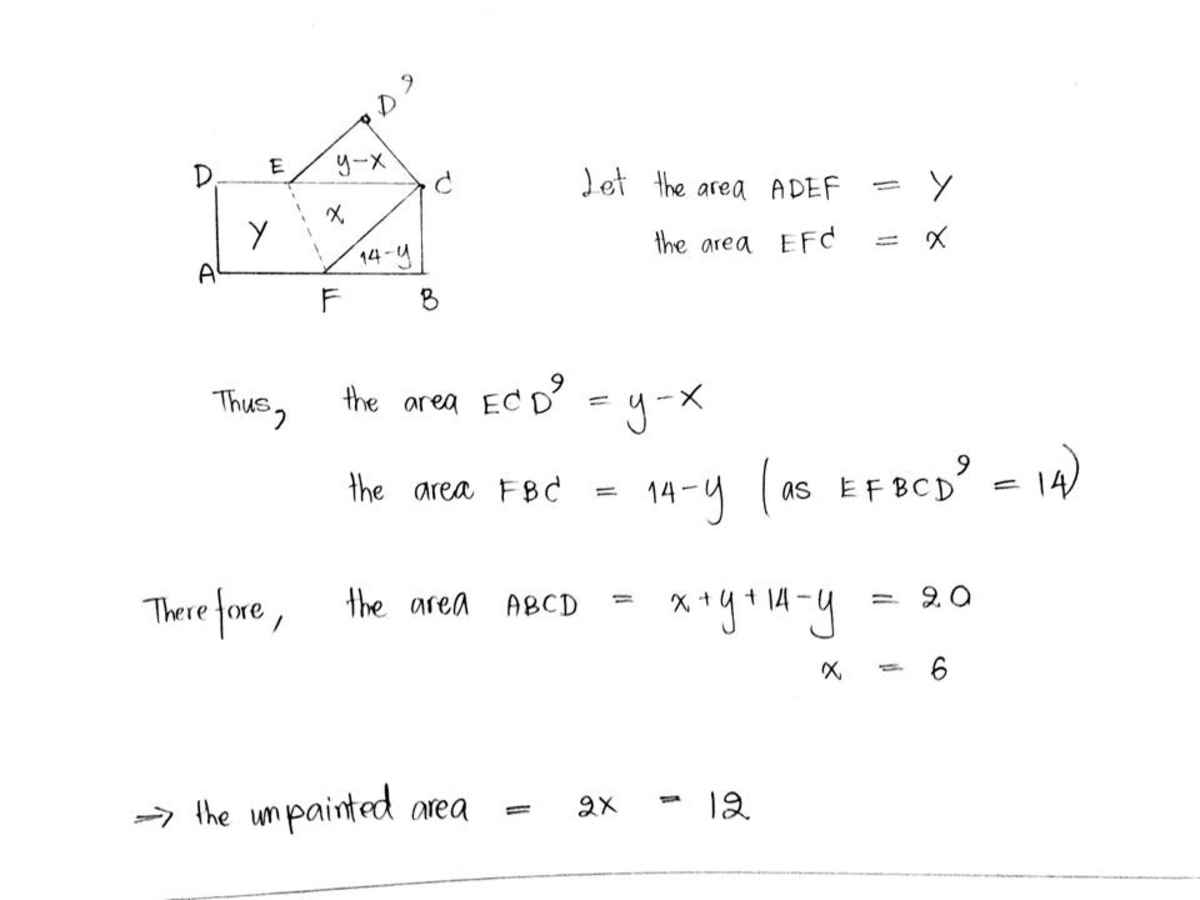
Undoing a pentagon
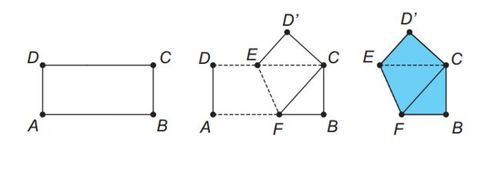 A white rectangular paper
A
B
C
D
with an area of
2
0
cm
2
is bent as shown, forming a pentagon
B
C
D
′
E
F
with an area of
1
4
cm
2
. If we paint both sides of this pentagon in blue and undo the fold, the rectangle will have an unpainted area. What is the area of this region?
A white rectangular paper
A
B
C
D
with an area of
2
0
cm
2
is bent as shown, forming a pentagon
B
C
D
′
E
F
with an area of
1
4
cm
2
. If we paint both sides of this pentagon in blue and undo the fold, the rectangle will have an unpainted area. What is the area of this region?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions

Moderator note:
Great solution! It's just a composite figure problem after all!
For completeness, how would one go about showing that [ E C B F ] = 2 1 [ A B C D ] ?
Thanks for the note!
For a very completed solution, I shall add the following content:
∵ In R t △ A E D a n d R t △ C E D ′ ,
{ A D = C D ′ D E = D ′ E
∴ R t △ A E D ≅ R t △ C E D ′ .
∴ A E = C E , and ∠ D E A = ∠ D ′ E C .
Also , ∵ ∠ D E F = ∠ D ′ E F ,
∴ ∠ A E F = ∠ C E F .
∵ C D ∥ A B ,
∴ ∠ C E F = ∠ E F A , ∠ D E F = ∠ E F B ,
∴ ∠ A E F = ∠ A F E = ∠ C E F = ∠ C F E ,
∴ A E = A F = C E = C F .
Also, in R t △ A D E a n d R t △ C B F ,
∵ { A E = C F A D = C B
∴ R t △ A D E ≅ R t △ C B F ,
∴ D E = F B .
∴ [ E C B F ] = 2 1 ( E C + B F ) × C B
= 2 1 ( A F + D E ) × A D = [ A D E F ] .
∵ [ E C B F ] + [ A D E F ] = [ A B C D ] ,
∴ [ E C B F ] = 2 1 [ A B C D ] .
Nice solution Punpun :)