A geometry problem by Jádson Bráz
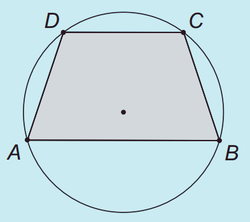 In the following figure,
is a trapezoid inscribed in a circle. The longer base
has length 16 cm, the shorter base
has length 10 cm, and the altitude of the trapezoid has length 9 cm. What is the radius of the circle, in centimeters?
In the following figure,
is a trapezoid inscribed in a circle. The longer base
has length 16 cm, the shorter base
has length 10 cm, and the altitude of the trapezoid has length 9 cm. What is the radius of the circle, in centimeters?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Drop perpendiculars from the center of the circle O on AB and CD. Let the perpendiculars meet AB and DC at E and F respectively. We know that Perpendiculars from center bisects a chord. So EB=8 and FC=5. Let FO= x , So EO=(9-x) Also, OC=OB=r (radius of circle)
Using Pythagoras Theorem, (FC)^2+(OF)^2=r^2 => (5)^2+(x)^2=r^2 .......eqn (1) (OE)^2+(EB)^2=r^2 => (9-x)^2+(8)^2=r^2 .......eqn(2)
Comparing eqn (1) and eqn (2) we get x= 20/3
Putting value of x in any of the eqations will give value of r which is equal to 25/3.