Colored Tiles And Tangent Circles

Geometry Level 3

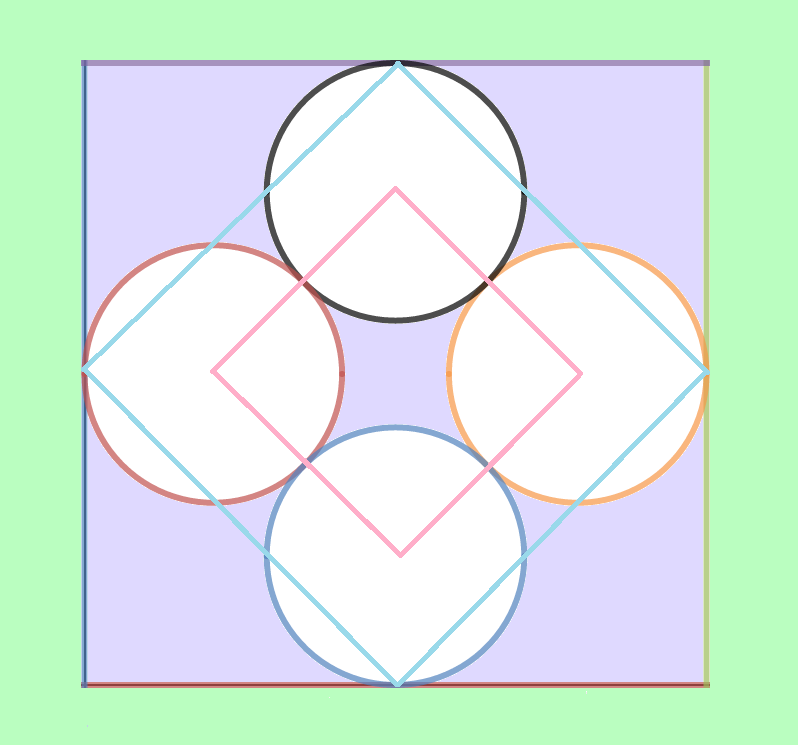
As shown in the figure, four circles are inscribed within a square. Each circle is tangent to both of its adjacent circles and the midpoint of the square's nearest side.

By connecting the midpoints for each of the square's sides, one creates a light blue square. Likewise, by drawing four line segments between each of the circles' centers, one creates a pink square. Find the ratio of the area enclosed by the larger blue square and the area enclosed by the smaller pink square. If this proportion can be expressed in the form $\frac { A }{ B } +\sqrt { C }$ , with $A$ , $B$ , and $C$ primes, find $A+B+C$ .

Details and Assumptions :

The area enclosed by the blue square includes the pink square as well.

This problem is original. The picture was produced from Desmos and MS Paint.

The answer is 7.

1 solution

Ahmad Saad
Feb 19, 2016

The area enclosed by the larger blue square is $2L^2$ .
The area enclosed by the larger blue square is $4R^2$ .

Figure shows that

$(2R)^2 = 2(L-R)^2 \Rightarrow R = (\sqrt2 - 1) L .$

And the ratio fo the two areas is

$\begin{aligned} \dfrac{2L^2}{4R^2} &=& \dfrac{2L^2}{4 [ L (\sqrt2-1) ] ^2} \\ &=& \dfrac12 (\sqrt2 + 1)^2 \\ &=& \dfrac32 + \sqrt2 \end{aligned}$

Thus we have $A = 3, B = 2, C = 2 \Rightarrow A+B+C=\boxed7$ .

Colored Tiles And Tangent Circles

This problem is original. The picture was produced from Desmos and MS Paint.

The answer is 7.

1 solution

0 pending reports