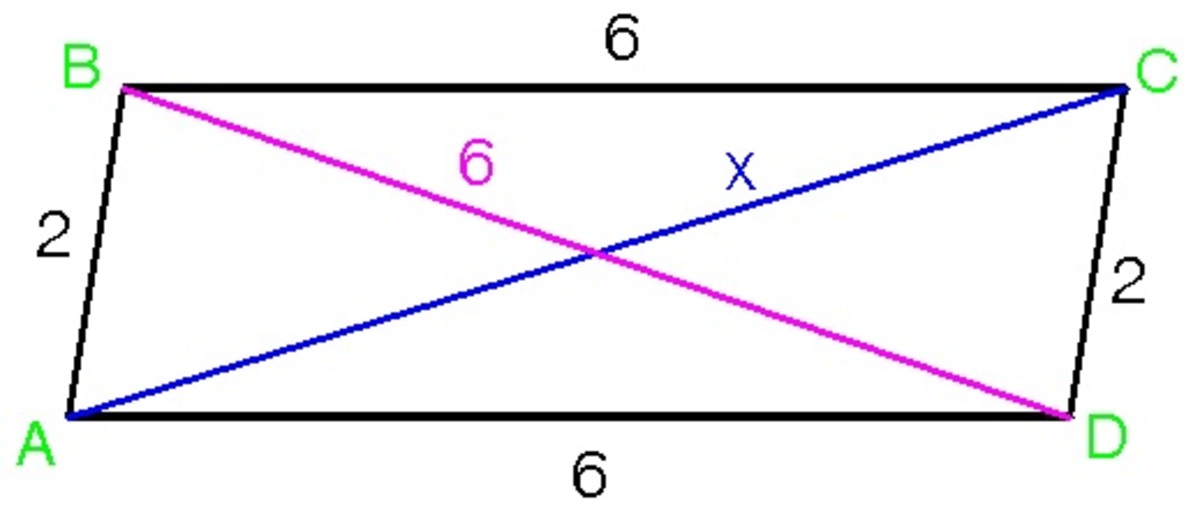
A geometry problem by Julian Yu

Let the parallelogram be $ABCD$ as shown in the diagram. Then the shorter diagonal is $AC$ and the longer diagonal is $BD$ . Let $\angle BAC = \angle ACD \theta$ . Then by cosine rule , we have:

$\begin{aligned} |BD|^2 & = |AB|^2+|AD|^2 - 2|AB||AD|\cos \angle BAD \\ x^2 & = 6^2+2^2 - 2(6)(2)\cos (\angle BAC + \angle CAD) & \small \color{#3D99F6} \text{Note that }\triangle ACD \text{ is isosceles.} \\ & = 40 - 24 \cos \left(\theta + \frac {180^\circ - \theta}2 \right) \\ & = 40 - 24 \cos \left(90^\circ + \frac \theta 2 \right) & \small \color{#3D99F6} \text{Note that } \cos (180^\circ -x) = - \cos x \\ & = 40 + 24 \cos \left(90^\circ - \frac \theta 2 \right) & \small \color{#3D99F6} \text{Note that } \cos (90^\circ -x) = \sin x \\ & = 40 + 24 \sin \frac \theta 2 & \small \color{#3D99F6} \text{Note that } \sin \frac \theta 2 = \frac 16 \\ & = 40 + 24 \times \frac 16 \\ & = 40 + 4 \\ & = \boxed{44} \end{aligned}$

Without Cosine Rule, The Relation Between The Diagonals & Sides Of A Parallelogram Is: $2(AB)^2$ + $2(BC)^2$ = $(AC)^{2}$ + $(BD)^{2}$ $\implies$ $2(2^2)$ + $2(6^2)$ = $6^2$ + $x^2$ $\implies$ $x^2 = 44$

Considering triangle ABD:

By Cosine Law

$6^2=2^2+6^2-2(2)(6)cos~A$

$\angle A=80.40593177^\circ$

It follows that,

$\angle B=\angle D=\dfrac{360-2(\angle A)}{2}=\dfrac{360-2(80.40593177)}{2}=99.59406823^\circ$

Considering triangle ACD:

By Cosine Law

$x^2=2^2+6^2-2(2)(6)cos~99.59406823=$ $\boxed{\color{#D61F06}44}$

$\triangle AEB$ is a right triangle, so $\cos\alpha=\frac{1}{6}$ .

$\beta=180^\circ-\alpha$ therefore $\cos\beta=-cos\alpha=-\frac{1}{6}$

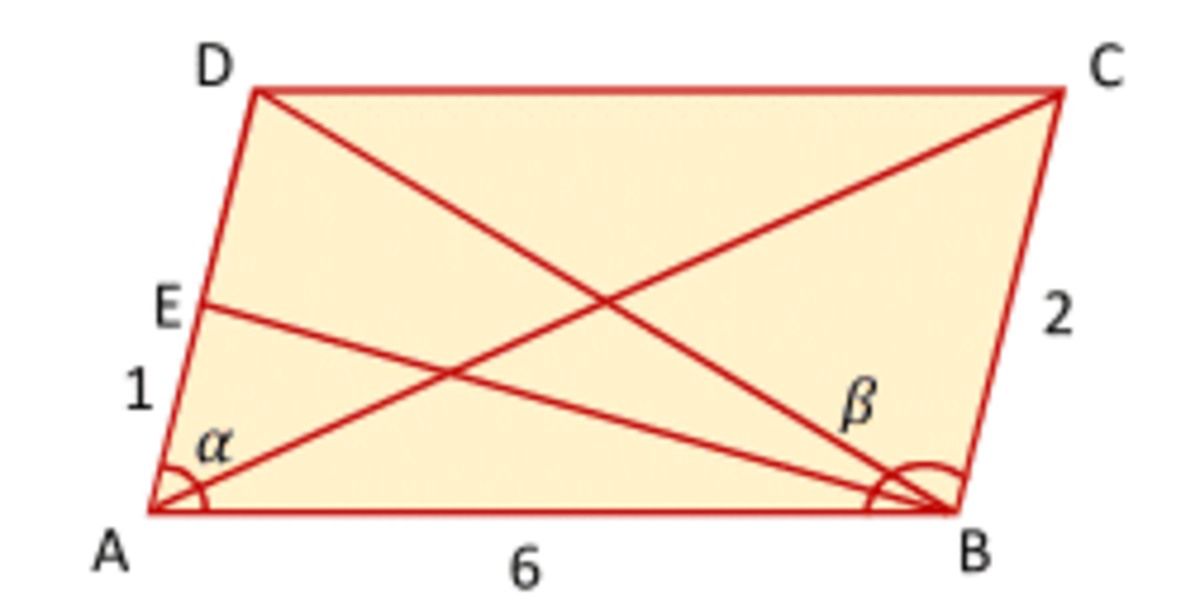From $\triangle ABC$ using law of cosines $AC^2=x^2=6^2+2^2-2\times6\times2\times \cos\beta=36+4+4=44$