Can I make more assumptions?
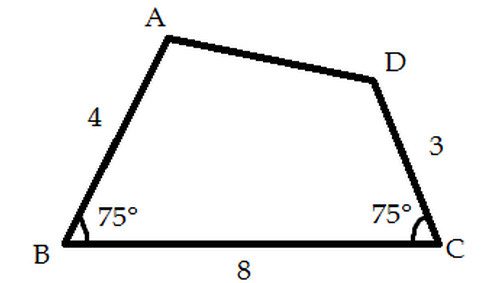 Given that quadrilateral
with side length
and angles
, find the area of quadrilateral
. Give your answer in unit squared.
Given that quadrilateral
with side length
and angles
, find the area of quadrilateral
. Give your answer in unit squared.
Note: Figure not drawn up to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
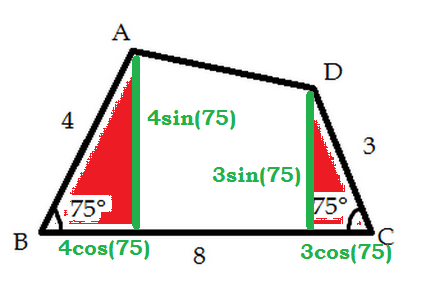
Drop a perpendicular from A to B C at point P . Next, drop a perpendicular from D to B C at point Q . Finally, draw a line parallel to B C through D , and let R be the point of intersection of this line and A P .
Then the area of the quadrilateral A B C D is the sum of the areas of triangles Δ A B P , Δ D Q C , Δ A R D and the rectangle R P Q D . Looking at these areas separately, we have:
(i) Area Δ A B P = 2 1 ∗ ( 4 sin ( 7 5 ∘ ) ) ( 4 cos ( 7 5 ∘ ) ) = 4 sin ( 1 5 0 ∘ ) = 2
(ii) Area Δ D Q C = 2 1 ( 3 sin ( 7 5 ∘ ) ) ( 3 cos ( 7 5 ∘ ) ) = 4 9 sin ( 1 5 0 ∘ ) = 8 9
(iii) Area Δ A R D = 2 1 ( A R ) ( R D ) = 2 1 ( A R ) ( P Q ) =
2 1 ( ( 4 − 3 ) sin ( 7 5 ∘ ) ) ( 8 − ( 4 + 3 ) cos ( 7 5 ∘ ) ) =
2 1 ( 8 sin ( 7 5 ∘ ) − 7 sin ( 7 5 ∘ ) cos ( 7 5 ∘ ) ) =
4 sin ( 7 5 ∘ ) − 4 7 sin ( 1 5 0 ∘ ) = 4 sin ( 7 5 ∘ ) − 8 7
(iv) Area rectangle R P Q D = ( R P ) ( P Q ) = 3 sin ( 7 5 ∘ ) ( 8 − 7 cos ( 7 5 ∘ ) ) =
2 4 sin ( 7 5 ∘ ) − 2 2 1 sin ( 1 5 0 ∘ ) = 2 4 sin ( 7 5 ∘ ) − 4 2 1 .
Adding these areas together gives us the area of A B C D to be
2 + 8 9 − 8 7 − 4 2 1 + 2 8 sin ( 7 5 ∘ ) = 2 8 sin ( 7 5 ∘ ) − 3 .
Now sin ( 7 5 ∘ ) = sin ( 4 5 ∘ + 3 0 ∘ ) = 2 2 ( 2 1 + 2 3 ) = 4 2 + 6 .
Thus the final area calculation is 7 6 + 7 2 − 3 .