Making aeroplanes
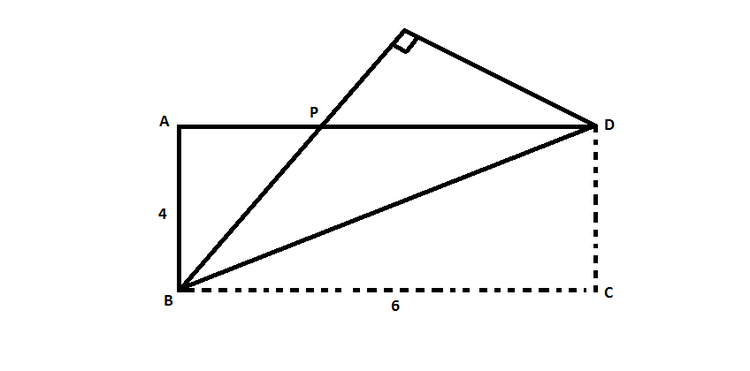 Given that the rectangle
A
B
C
D
is folded along the diagonal
B
D
, where
A
B
=
4
and
B
C
=
6
, find the area of the triangle
P
B
D
.
Given that the rectangle
A
B
C
D
is folded along the diagonal
B
D
, where
A
B
=
4
and
B
C
=
6
, find the area of the triangle
P
B
D
.
Note: Figure not drawn to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
You can simplify this solution by realizing that a r e a o f t r i a n g l e P B D = a r e a o f t r i a n g l e A B D − a r e a o f t r i a n g l e P A B and that the triangle ABD have the areas of 12, via a r e a = 2 1 b a s e ∗ h e i g h t . The area of triangle PAB can be solved vy solving for the side, x = 3 5 as shown above and reapplying the area formula gives the area of 3 1 0 for the triangle PAB. Thus the area of triangle PBD is 1 2 − 3 1 0 = 3 2 6
We define x and y as the following: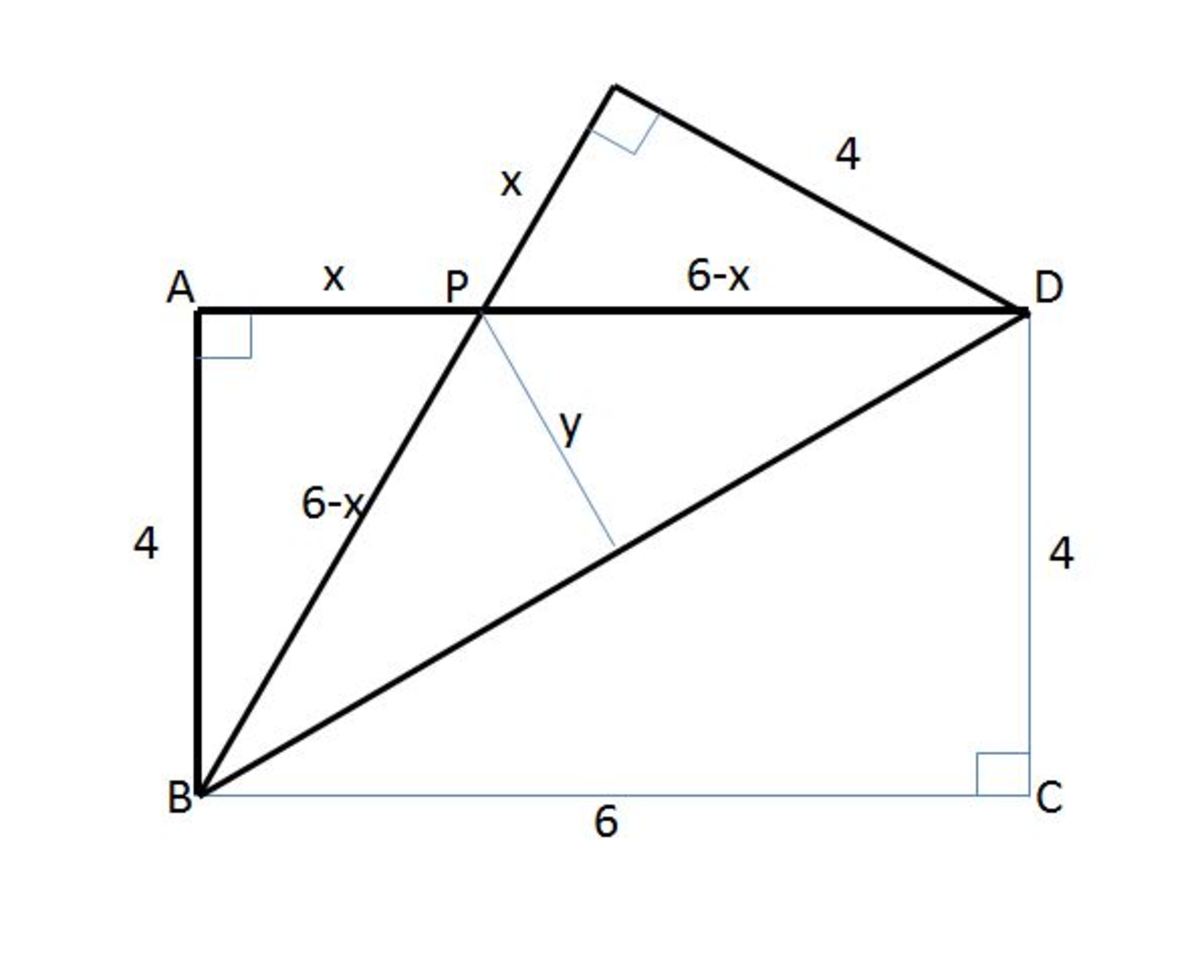 From the Pythagorean Theorem, we get
x
2
+
4
2
=
(
6
−
x
)
2
x
2
+
1
6
=
3
6
−
1
2
x
+
x
2
x
=
3
5
From the Pythagorean Theorem, we get
x
2
+
4
2
=
(
6
−
x
)
2
x
2
+
1
6
=
3
6
−
1
2
x
+
x
2
x
=
3
5
To find the length of the side B D ˉ , we apply the same theorem and get 6 2 + 4 2 = ( B D ˉ ) 2 ( B D ˉ ) 2 = 5 2 B D ˉ = 2 1 3
To find the value of y,
[ 2 1 ( 2 1 3 ) ] 2 + y 2 = ( 6 − 3 5 ) 2 1 3 + y 2 = 9 1 6 9 y 2 = 9 5 2 y = 3 2 1 3
Finally, we use A = 2 b h to find the area of P B D
A = 2 2 1 3 ( 3 2 1 3 ) A = 3 5 2 ( 2 1 ) A = 3 2 6
This is my first solution, so any feedback is appreciated! :)