Midpoints save the Day!
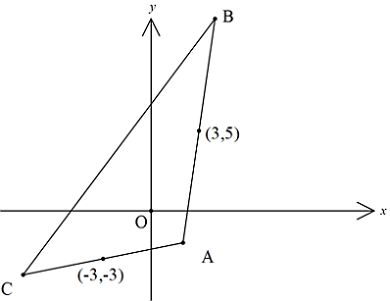
If the midpoints of the sides A B and A C of triangle A B C are ( 3 , 5 ) and ( − 3 , − 3 ) respectively, then find the length of B C .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
2 x A + x B = 3 ; by definition of midpoint. ⟹ x B = 6 − x A
2 x A + x C = − 3 ; by definition of midpoint ⟹ x c = − 6 − x A
2 y A + y B = 5 ; by definition of midpoint ⟹ y B = 1 0 − y A
2 y A + y C = − 3 ; by definition of midpoint ⟹ y C = − 6 − y A
Thus: || B C || = ( x C − x B ) 2 + ( y C − y B ) 2 ) = ( 6 + 6 ) 2 + ( 1 0 + 6 ) 2 ) = 2 0
Let A,B,C be the vertices of the triangle and let the coordinates of A,B,C be (x1,y1), (x2, y2),(x3, y3) respectively. Applying midpiont theorm,
Then (x1+x2)/2=3 which implies x1+x2=6--------(i)
(x1+x3)/2=-3 which implies x1+x3=-6--------(ii)
solving i and ii
x3-x2=12----------(I)
similarly,
(y1+y2)/2=5 which implies y1+y2=10------(i)
(y1+y3)/2=-3 which implies y1+y3=-6--------(ii)
solving (i) and (ii)
y3-y2=16--------------(II)
length of BC= root of (x3-x2)^2+(y3-y2)^2
which is 20 units
Moderator note:
Can you find the 1-line solution to this problem?
Hint: How does the length of BC relate to the length between the midpoints?
@Keerthi Reddy I've converted your comment in the report forum into an actual solution.
This is a simple English answer haha.
It is given that the coordinates are midpoints of the line. This is a major clue.
Imagine a 2nd triangle formed by these midpoints. That is, draw a line (a hypotenuse) with (3,5) as start and (-3,-3) as end. The two triangles are similar in size (you can do the proving for me lol).
As the coordinates are midpoints, then the lengths of the 2nd triangle are half the lengths of AC and AB. This means, the hypotenuse of the 2nd triangle is also half the length of BC.
Using the distance formula, you can calculate that the distance between the midpoints is 10 units. Therefore, BC is twice the length of 10 which gives the final answer of 20 units. BC=20