Finding the Circumradius

Geometry Level 2

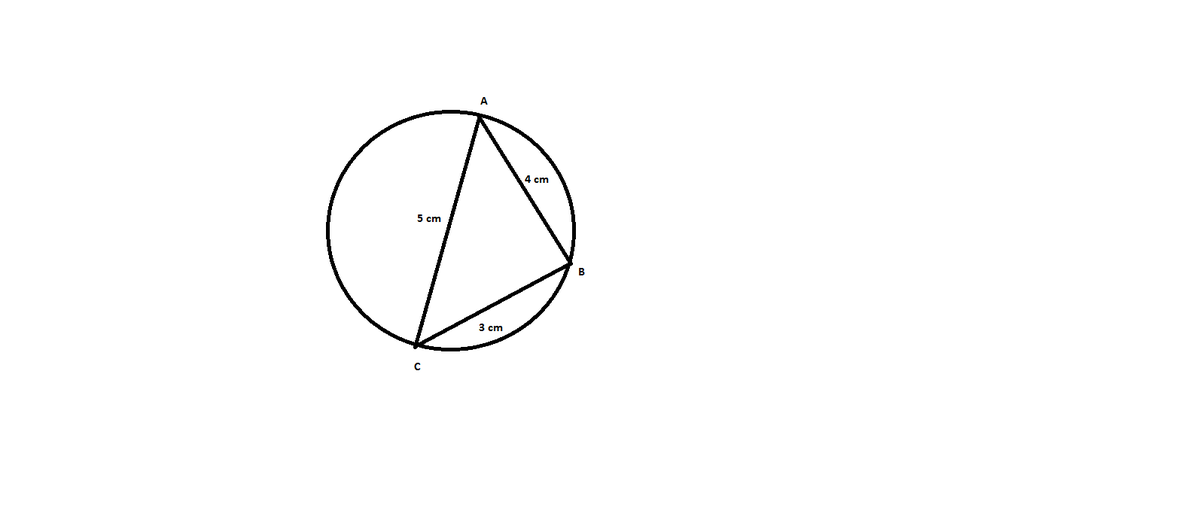
What is the circumradius of a triangle which has sides of length 3, 4, and 5 units?

2.5 units 3 units 2.75 units 2 units

Krishna Keshav by Krishna Keshav , 24, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Here a , b , c a,b,c are sides of △ \triangle , r r radius of circle inscribed and s s semi-perimeter of triangle.

r × s = Area of △ r×s=\text{Area of }\triangle
r × s = s ( s − a ) ( s − b ) ( s − c ) r×s=\sqrt{s(s-a)(s-b)(s-c)}
r = ( s − a ) ( s − b ) ( s − c ) r=\sqrt{(s-a)(s-b)(s-c)}
r = ( 3 ) × ( 2 ) × ( 1 ) r=\sqrt{(3)×(2)×(1)}
r = 6 = 2.5 r=\sqrt{6}=\boxed{2.5}

4 Helpful 0 Interesting 0 Brilliant 0 Confused

We could also just note that, since a 3 / 4 / 5 3/4/5 triangle is right-angled, the hypotenuse corresponds to a diameter of the circumcircle, (by Thales' theorem ), and thus the circumradius is one-half the length of the hypotenuse, namely 5 / 2 = 2.5 5/2 = 2.5 units.

Brian Charlesworth - 5 years, 5 months ago

Log in to reply

That's also nice Sir .

A Former Brilliant Member - 5 years, 5 months ago

This was correct one.. I was not able to type that solution

Krishna Keshav - 5 years, 4 months ago
Harshendu Mahto
Jan 17, 2016

It is clear that 3,4,5 are pythagorean triplets.

Therefore the triangle must be a right angled triangle.

We know that in a circle angle in a semi circle is a right angle.

So AC must be the diameter. but AC = 5

and, diameter/2 = radius

Therefore ,

radius = 5/2 = 2.5

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Good solution Harshendu . I also tried the same.

abhigyan adarsh - 5 years, 4 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...