A geometry problem by Kulsoom Rizvi
Geometry
Level
4
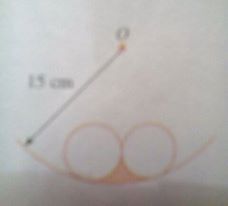
The diagram shows two identical circles of radius 5cm touching each other externally and a larger circle, centre O and radius 15cm, touching internally. calculate the area of the shaded region correct to 1 decimal place.
The answer is 22.1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The three centers form an equilateral triangle of sides 10 cm. So the sector of interest from big circle has an area of + 3 6 0 6 0 ∗ π ∗ 1 5 2 .
The equilateral triangle is not shaded. So its area − 4 3 ∗ π ∗ 1 0 2
Sectors each of the small circles that is not shaded makes 120^o at their centers. So their areas − 2 ∗ 3 6 0 1 2 0 ∗ π ∗ 5 2 .
Shaded area = + 3 6 0 6 0 ∗ π ∗ 1 5 2 − 4 3 ∗ π ∗ 1 0 2 − 2 ∗ 3 6 0 1 2 0 ∗ π ∗ 5 2 = 2 2 . 1 4 8