A geometry problem by Kunal Maan
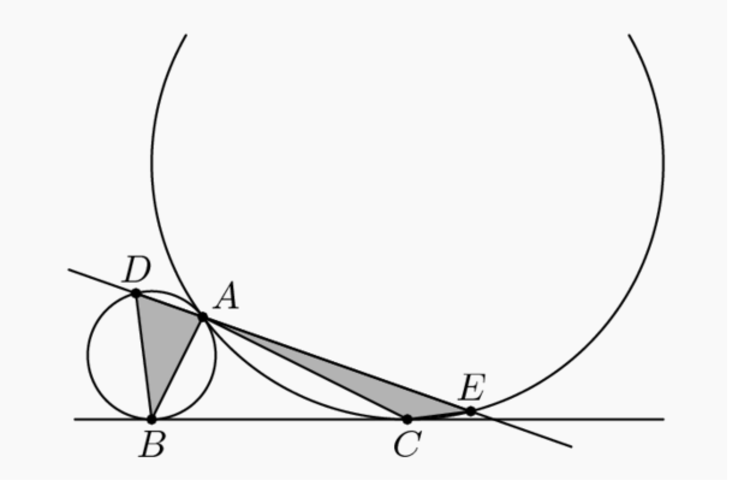 Circles
and
have radii 1 and 4 respectively and are externally tangent at point
. Point
is on
and point
is on
such that
is a common external tangent of the two circles. A line
through
intersects
again at
and intersects
again at
. Points
and
lie on the same side of the line
and the areas of
and
are equal. This common area is
, where
are co-prime positive integers. Find the value of
.
Circles
and
have radii 1 and 4 respectively and are externally tangent at point
. Point
is on
and point
is on
such that
is a common external tangent of the two circles. A line
through
intersects
again at
and intersects
again at
. Points
and
lie on the same side of the line
and the areas of
and
are equal. This common area is
, where
are co-prime positive integers. Find the value of
.
The answer is 129.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
By homothety, we deduce that $AE = 4 AD$. (The proof can also be executed by similar triangles formed from dropping perpendiculars from the centers of $P$ and $Q$ to $l$.) Therefore, our equality of area condition, or the equality of base times height condition, reduces to the fact that the distance from $B$ to $l$ is four times that from $C$ to $l$. Let the distance from $C$ be $x$ and the distance from $B$ be $4x$. Let $P$ and $Q$ be the centers of their respective circles. Then dropping a perpendicular from $P$ to $Q$ creates a $3-4-5$ right triangle, from which $BC = 4$ and, if $\alpha = \angle{AQC}$, that $\cos \alpha = \dfrac{3}{5}$. Then $\angle{BPA} = 180^\circ - \alpha$, and the Law of Cosines on triangles $APB$ and $AQC$ gives $AB = \dfrac{4}{\sqrt{5}}$ and $AC = \dfrac{8}{\sqrt{5}}.$ Now, using the Pythagorean Theorem to express the length of the projection of $BC$ onto line $l$ gives 5 1 6 − 1 6 x 2 + 5 6 4 − x 2 = 1 6 − 9 x 2 . Squaring and simplifying gives ( 5 1 − x 2 ) ( 5 6 4 − x 2 ) = x 2 , and squaring and solving gives $x = \dfrac{8}{5\sqrt{13}}.$ By the Law of Sines on triangle $ABD$, we have sin A B D = 2 . But we know $\sin A = \dfrac{4x}{AB}$, and so a small computation gives $BD = \dfrac{16}{\sqrt{65}}.$ The Pythagorean Theorem now gives A D = B D 2 − ( 4 x ) 2 + A B 2 − ( 4 x ) 2 = 1 3 4 , and so the common area is $\dfrac{1}{2} \cdot \frac{4}{\sqrt{13}} \cdot \frac{32}{5\sqrt{13}} = \frac{64}{65}.$ The answer is $\boxed{129}.$