3 0 ∘ Is Always Good
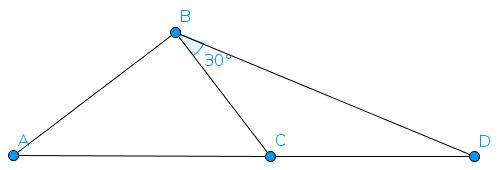
A B = C D = 1 , m ∠ A B C = 9 0 ∘ , m ∠ C B D = 3 0 ∘ . A , C , and D , are collinear. A C can be represented in the simplest form as a 1 / b , where a and b are positive integers such that a is minimized. Find a + b .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let A C = x , B D = z and ∠ A C B = θ . Apply law of cosines on △ A B D :
( x + 1 ) 2 = 1 + z 2 − 2 ( 1 ) ( z ) cos 1 2 0 ∘ ⟹ x 2 + 2 x = z 2 + z
Apply law of sines on △ A B C :
sin θ = x 1
Then on △ B C D :
sin 3 0 ∘ sin ( π − θ ) = 1 z ⟹ sin θ = 2 z
Then, z = x 2 .
Combining both equations we get:
x 2 + 2 x = ( x 2 ) 2 + x 2
x 4 + 2 x 3 − 2 x − 4 = 0 ⟹ ( x + 2 ) ( x 3 − 2 ) = 0 .
Finally, x = 3 2 .
Relevant wiki: Similar Triangles - Problem Solving - Medium
We extend the straight line A B to the point E such that the △ B A C ∼ △ B E D . Hence, like △ B A C , the △ B E D is also a right triangle with ∠ B E D = 9 0 ∘ .
Let m denote the distance A E , then cos ( ∠ E A D ) = A D A E ⇒ cos ( 1 8 0 ∘ − 9 0 ∘ − 3 0 ∘ ) = A D m ⇒ A D = 2 m .
By Pythagorean theorem , ( E D ) 2 = ( A D ) 2 − ( A E ) 2 ⇒ E D = 3 m .
Let A C = h , B C = x ⇒ 1 2 + h 2 = x 2 .
Since △ B A C ∼ △ B E D , then B E A B = B D B C ⇒ 1 + m 1 = 1 + x x = 1 + 1 / x 1 ⇒ m = x 1 .
Similarly, E D A C = B D B C ⇒ 3 m h = 1 + x x . With m = x 1 , then h = 1 + x 3 .
Because 1 2 + h 2 = x 2 , then 1 + ( 1 + x ) 2 3 = x 2 ⇒ x 4 + 2 x 3 = 2 x + 4 ⇒ ( x + 2 ) x 3 = 2 ( x + 2 ) ⇒ x 3 = 2 ⇒ x = 2 1 / 3 .