Optimize Peripheral Vision
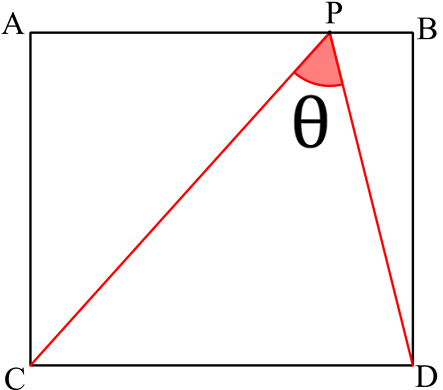
A B D C is a rectangle and P is a point on the straight line A B . The lengths of A C and A B are 1 and 3 2 , respectively. Find the maximum value of θ to the nearest integer.
Enter your answer in degrees.
Note : Image drawn not up to scale.
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Plz explain what is am gm method
Log in to reply
Check out the arithmetic mean - geometric mean wiki page.
An arithmetic mean of n positive reals is greater than or equal to their geometric mean (arithmetic mean - their sum divided by n; geometric mean - n-th root of their product)
Set x = A P and Q ∈ [ C D ] such as ( P Q ) / / ( A C ) .
Set θ 1 ( x ) = ∠ C P Q = arctan ( x ) and θ 2 ( x ) = ∠ Q P D = arctan ( 3 2 − x )
Then θ ( x ) = θ 1 ( x ) + θ 2 ( x ) = arctan ( x ) + arctan ( 3 2 − x )
θ ′ ( x ) = ( 1 + x 2 ) ( 1 + ( 3 2 − x ) 2 ) 2 ( 3 1 − x ) ( 3 2 )
θ is then maximum when x = 3 1
Finally, θ m a x = θ ( 3 1 ) = 2 arctan ( 3 1 ) = 6 0 ∘
PS : According to the figure, it is rectangle ABDC, not ABCD.
It does not necessarily imply that θ ( x ) is maximized when θ ′ ( x ) = 0 . You still need to show that it is true by applying the second derivative test .
Nice! It's correct. You can also solve this problem using AM and GM.
θ = α + β
t g θ = t g ( α + β ) = 1 − t g α ⋅ t g β t g α + t g β ⟹ t g ( α + β ) = 1 − A P ⋅ P B A P + P B = 1 − A P ⋅ P B 3 2
By the AM GM inequality:
2 a + b ≥ a b
we know that, to maximize the product A P ⋅ P B , we must have A P = P B .
Now it's easy to calculate θ :
t g θ = 1 − ( 3 1 ) 2 3 2 = 3 ⟹ θ = 6 0 º