A geometry problem by Majed Musleh
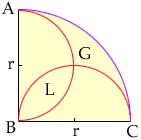 In the above image if
Find the area of
In the above image if
Find the area of
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First i will write the equations of the three circles A − x 2 + y 2 = 4 0 0 B − ( x − 1 0 ) 2 + y 2 = 1 0 0 C − x 2 + ( y − 1 0 ) 2 = 1 0 0 Now the area L = G how? G = t h e a r e a o f q u a r t e r A B C − t h e a r e a o f t h e s e m i c i r c l e B C − t h e s e m i c i r c l e A C + L we add L because we substract it twice when we substract the two semicircles G = π 4 2 0 2 − π 2 1 0 2 − π 2 1 0 2 + L do the calculation ... = > G = L now we need to find the points of intersection from eq. B and eq. C x 2 − 2 0 x + 1 0 0 + y 2 = x 2 + y 2 − 2 0 y + 1 0 0 => x = y =>substitute in eq. B we get y = 0 = > x = 0 o r y = 1 0 = > x = 1 0 the points of intersection leads us to drow the square with side length 1 0 as shown in the photo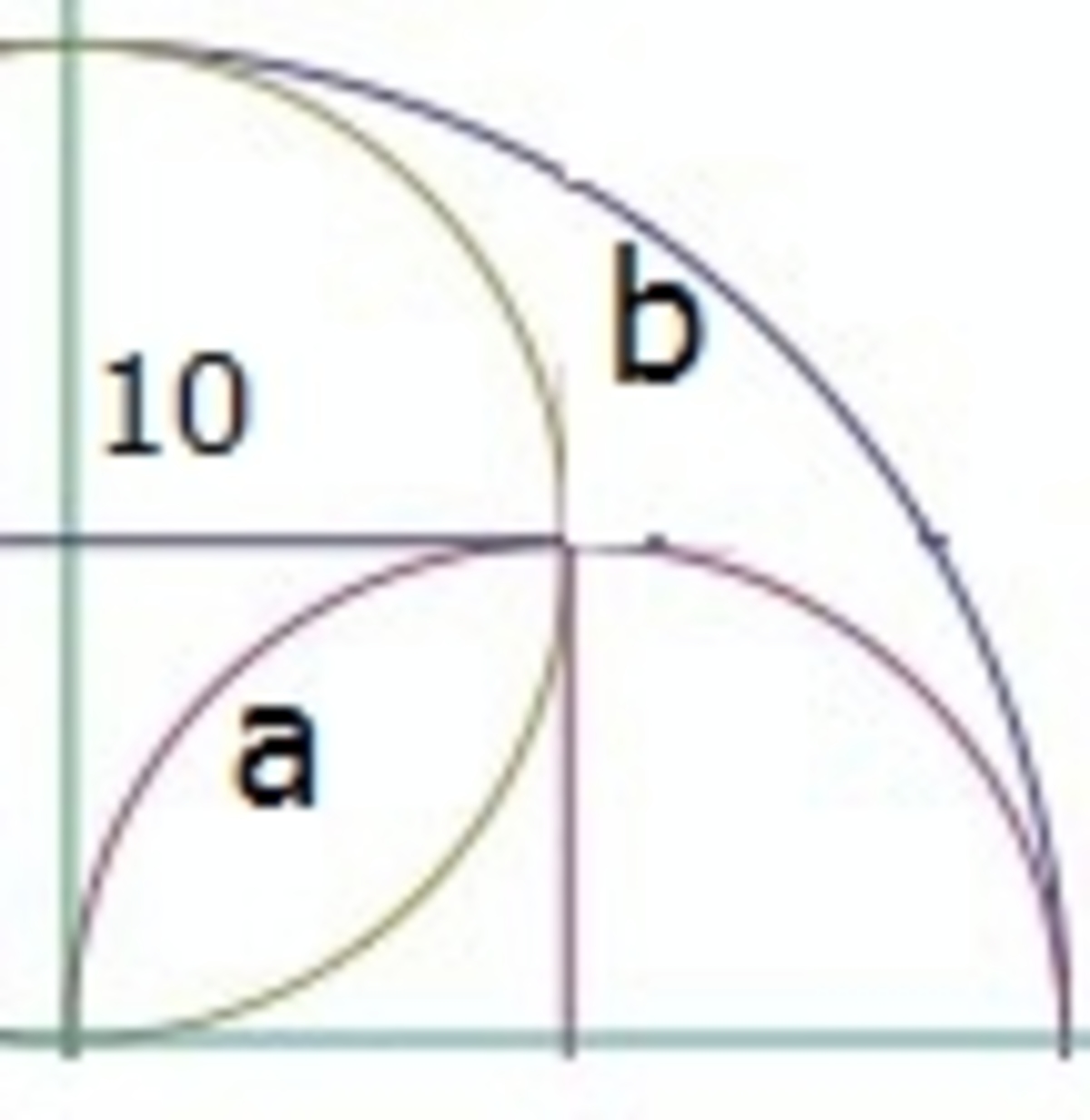 now the area of
G
=
t
h
e
a
r
e
a
o
f
q
u
a
r
t
e
r
A
B
C
−
t
h
e
a
r
e
a
o
f
t
h
e
s
q
u
a
r
e
−
2
t
h
e
a
r
e
a
o
f
t
h
e
q
u
a
r
t
e
r
o
f
c
i
r
c
l
e
w
i
t
h
r
=
1
0
G
=
π
4
2
0
2
−
1
0
2
−
2
π
4
1
0
2
=
5
0
π
−
1
0
0
=
5
0
(
π
−
2
)
Finally
L
+
G
=
2
∗
5
0
(
π
−
2
)
=
1
0
0
(
π
−
2
)
now the area of
G
=
t
h
e
a
r
e
a
o
f
q
u
a
r
t
e
r
A
B
C
−
t
h
e
a
r
e
a
o
f
t
h
e
s
q
u
a
r
e
−
2
t
h
e
a
r
e
a
o
f
t
h
e
q
u
a
r
t
e
r
o
f
c
i
r
c
l
e
w
i
t
h
r
=
1
0
G
=
π
4
2
0
2
−
1
0
2
−
2
π
4
1
0
2
=
5
0
π
−
1
0
0
=
5
0
(
π
−
2
)
Finally
L
+
G
=
2
∗
5
0
(
π
−
2
)
=
1
0
0
(
π
−
2
)