Compare the areas
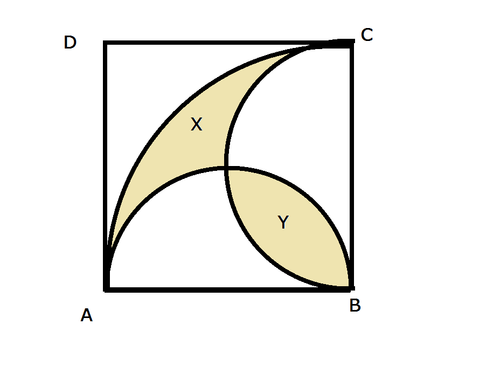 ABCD is a square.What is the ratio of area
X
to area
Y
?
ABCD is a square.What is the ratio of area
X
to area
Y
?
The answer is 1.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
how is this level one...
I got this incorrect thought i answered 1 😢
Let the center of the square be O
Let the area of the region OCB = a
the area of the region OCB = the area of the region OAB = a
Let the length of the side of the square be 2r
a + y =(1/2)(Pi) (r^2).............................. (1)
a + x = (1/4)(Pi)[(2 r)^2] -(1/2)(Pi) (r^2) =(1/2) (Pi) (r^2) .......................... (2)
From (1), (2) we get
x = y
So
x : y = 1 : 1
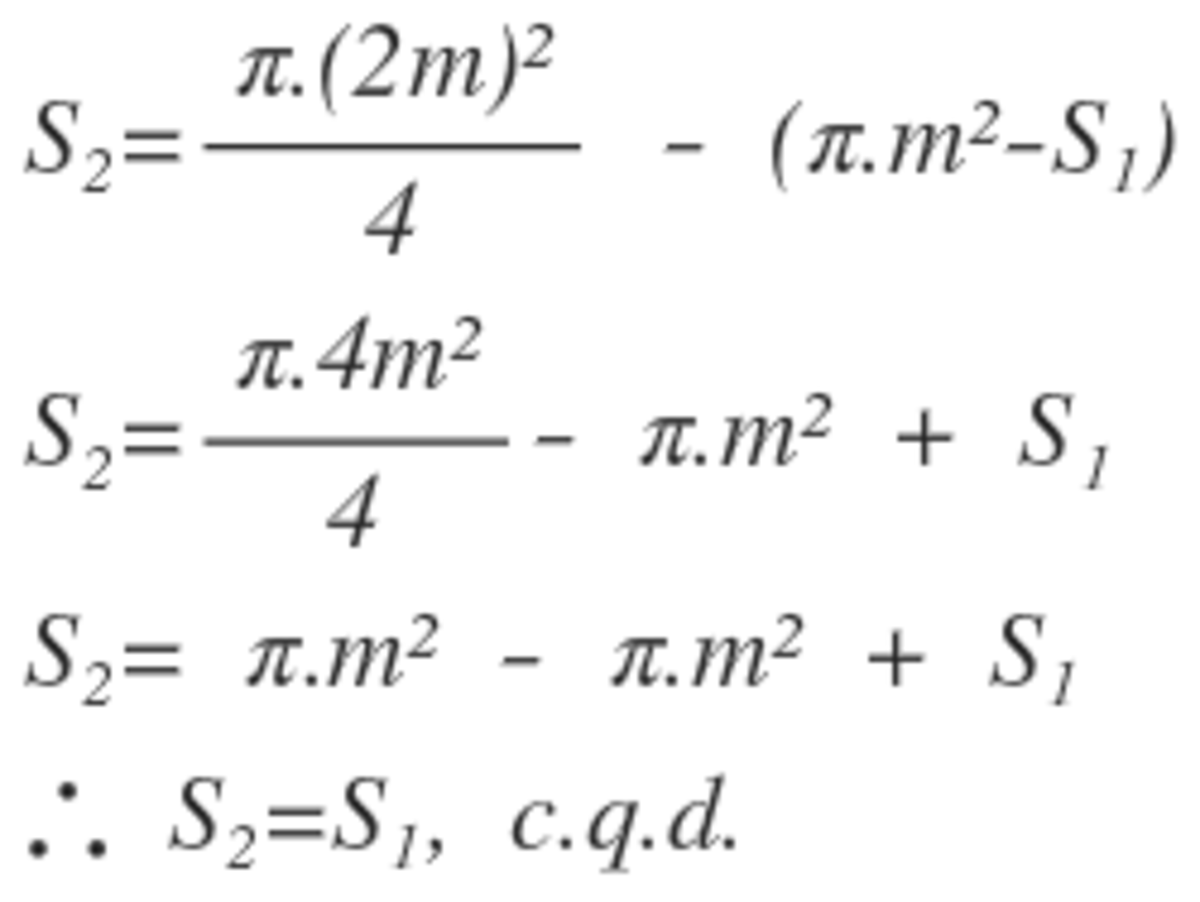
Let's call X=S1 and Y=S2
X=S1 and Y=S2, so S1=S2 means that Y=X, thus X/Y = 1
Let the center of the square be O , the midpoints of B C and A B be P and Q respectively and the side length of the square be a . We note that:
y = 2 ( Area of Quadrant Q O B − Area of △ Q O B )
= 2 [ 4 1 ( 2 π a ) 2 − 2 1 ˙ 2 a ˙ 2 a ] = 8 π a 2 − 4 a 2
x = Area of Quadrant A C B − Area of Semicircle A O B − Area of Semicircle C O B + y
= 4 1 ˙ π a 2 − 2 ( 2 1 ˙ 4 π a 2 ) + 8 π a 2 − 4 a 2 = 8 π a 2 − 4 a 2 = y
Therefore, y x = 1
X=quadrantACB MINUS THE SUM OF THE 2 SEMI CIRCLES +Y SO X=Y
The area of the quadrant A B C minus the areas of semicircles with diameters A B and B C gives us x − y . But this difference of areas equals 4 ( π ) ( a ) 2 − 2 ∗ 2 ( π ) ( a / 2 ) 2 = 0 . Hence x − y = 0 , and x : y = 1 .
The square ABCD has side "a". There are two semi-circles of radius 2 a and area S 1 each and a quarter of a circle of radius "a" and area S 2 . Hence:
-
S 1 = π × 8 a 2
-
S 2 = π × 4 a 2
Thus, observing the areas in the figure we can affirm that:
X = S 2 - S 1 - ( S 1 - Y)
Hence:
X = π 4 a 2 - 2 π 8 a 2 + Y
X = π 4 a 2 - π 4 a 2 + Y
X = 0 + Y
X = Y Then Y X = 1
If we analyse the two areas, we can see that
Area X = Area of Quadrant - [Sum of Area of Two Semi-circles] + Area Y )
Let
r = A B = B C = C D = D A be the length of the side of square ABCD.
We can also see that r is the length of the radius of the circle where the quadrant ABC is derived and r is also the diameter of a circle where the two semicircles are derived.
A r e a X = 4 1 π A B 2 − [ 2 1 π ( 2 A B ) 2 + 2 1 π ( 2 B C ) 2 ] + A r e a Y
A r e a X = 4 1 π r 2 − [ 2 1 π ( 2 r ) 2 + 2 1 π ( 2 r ) 2 ] + A r e a Y
A r e a X = 4 1 π r 2 − [ 2 1 π 4 r 2 + 2 1 π 4 r 2 ] + A r e a Y
A r e a X = 4 1 π r 2 − 4 1 π r 2 + A r e a Y
A r e a X = A r e a Y
So the ratio of the two areas is 1.0.
To calculate x you find the area of the large quarter - circle and subtract the area of the overlapping smaller semi-circles. Of course if we just call the area of the two semi-circle π r 2 then we have counted y twice. So the area must be π r 2 - y . ∴ x = π r 2 − ( π r 2 − y ) = y ⇒ y x = 1

First observe that the area of the quarter circle with centre B is made up of
area X + the area of the two semi circles - area Y
The area Y needs to be taken away because it has been counted twice, once in each semi circle.
Since we are looking for a ratio we can choose any scale we like to measure the problem. To ease the calculations suppose the square has a side of 2 units.
Then the big quarter circle has area 4 1 π 2 2 = π
Each semi circle has area 2 1 π 1 2 = 2 π
So by the above observation
π = x + π − y and so
x = y
and so the required ratio is 1