A geometry problem by mario dawi

Geometry Level 2

A large helium balloon is tethered to the ground by two taut lines. One line is 100 feet long and makes an 80 ° angle with the ground. The second line makes a 40 ° angle with the ground. How long is the second line (x), to the nearest foot? How far apart are the tethers (y)?

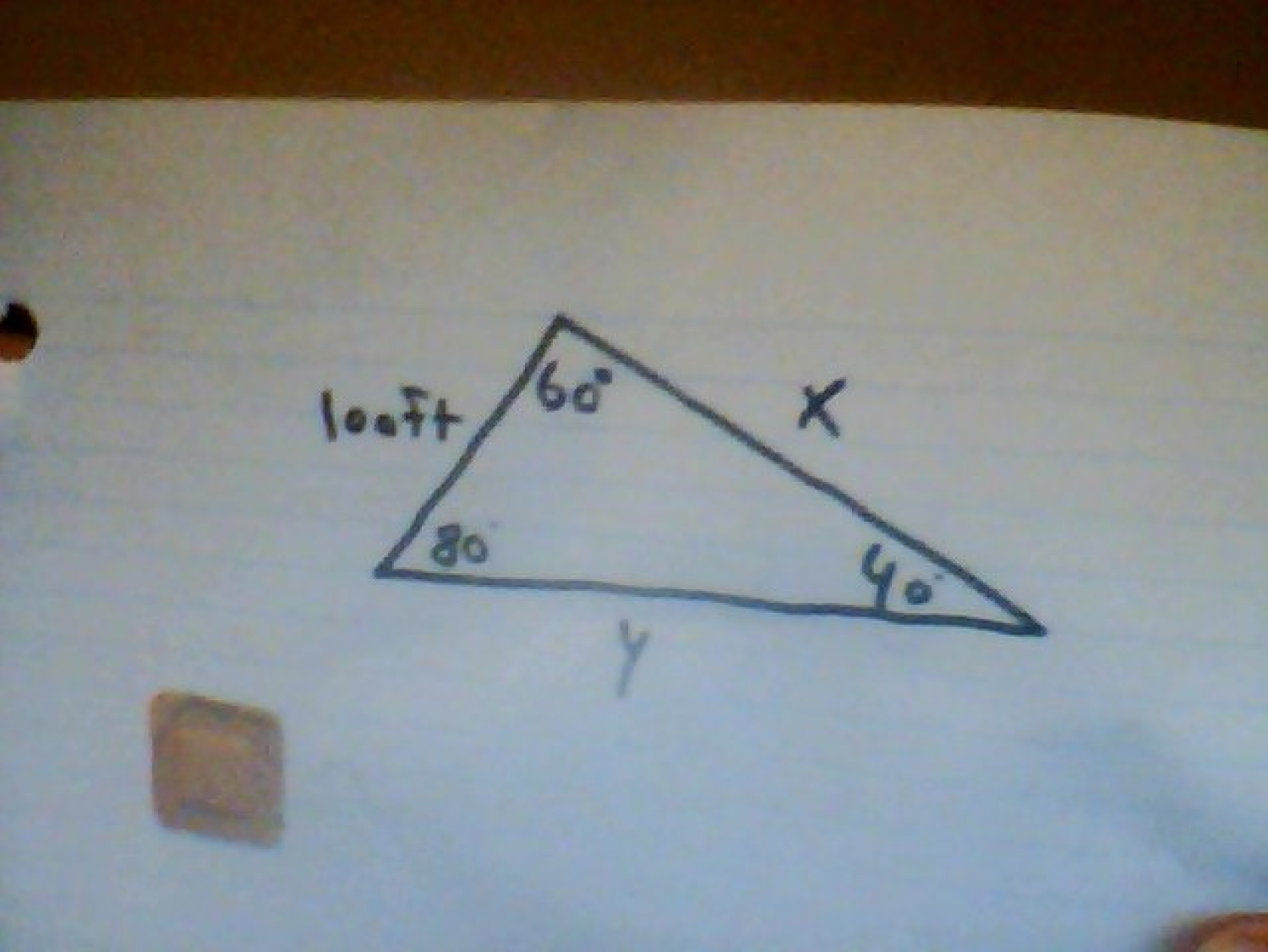
y=95 x=105 y=205 x=150 y=135 x=153 y=125 x=142

Mario Dawi by mario dawi , 22, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

By Sine Rule , we have

x sin ⁡ 80 = 100 sin ⁡ 40 \dfrac{x}{\sin 80}=\dfrac{100}{\sin 40}

x = sin ⁡ 80 sin ⁡ 40 × 100 ≈ 153 x=\dfrac{\sin 80}{\sin 40} \times 100 \approx \boxed{153}

By Sine Rule again, we have

y sin ⁡ 60 = 100 sin ⁡ 40 \dfrac{y}{\sin 60}=\dfrac{100}{\sin 40}

y = sin ⁡ 60 sin ⁡ 40 × 100 ≈ 135 y=\dfrac{\sin 60}{\sin 40} \times 100 \approx \boxed{135}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

By law of sines, we have

x sin ⁡ 80 = 100 sin ⁡ 40 \dfrac{x}{\sin~80}=\dfrac{100}{\sin~40} ⟹ \color{#D61F06}\large{\implies} x = 153 \color{plum}\boxed{x=153}

y sin ⁡ 60 = 100 sin ⁡ 40 \dfrac{y}{\sin~60}=\dfrac{100}{\sin~40} ⟹ \color{#D61F06}\large{\implies} y = 135 \color{plum}\boxed{y=135}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...